Para o circuito mostrado na Figura 24-36...
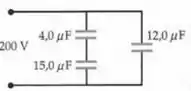
Os capacitores foram todos descarregados antes de serem conectados à fonte de tensão. Determine
(a) a capacitância equivalente da combinação
(b) a carga armazenada na placa carregada positivamente de cada capacitor
(c) a tensão em cada capacitor, e;
(d) a energia armazenada em cada capacitor.
Passo 1
Cara... Antes de falarmos sobre esse circuito do problema...
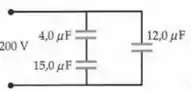
Repare que esse é um problema típico de associação de dois capacitores em série (capacitores e ) com um capacitor em paralelo (). Então, antes de falar desse circuito, vamos falar de um circuito geral desse tipo...
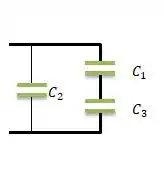
Passo 2
A capacitância resultante (equivalente ) seria a junção do (que é a equivalência da parte série) em paralelo com o , isto é...
OBS: O símbolo significa paralelo. Sabemos que em paralelo as capacitâncias se soma...
Para encontrar a , basta se lembrar de que capacitores em série possuem capacitância equivalente () através da fórmula...
Então...
Passo 3
Beleza, agora que já passamos por esse passo interno, podemos determinar o que queremos no exercício que é o ...

Fazendo então o paralelo entre e . Em paralelo, a resultante pode ser dada pela soma...
Então...
Passo 4
Considerando agora o nosso circuito...
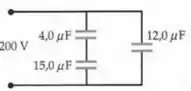
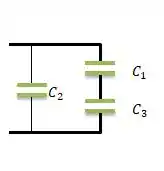
Podemos falar que...
Então a capacitância resultante será...
Passo 5
Basicamente nesse item, queremos a carga em cada capacitor. De cara, já podemos dizer que já que as cargas estão em série. Para encontrar a carga em série então...
Como...
E a tensão em cima dos dois capacitores em série é ...
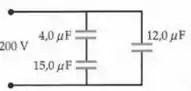
Então...
A carga positiva em cima do capacitor de e então é igual a .
Passo 6
Já para o capacitor de ...
Passo 7
A tensão em cada capacitor pode ser dada por...
Em cima do capacitor de que está em série...
E em cima do capacitor que também está em série como o capacitor de será...
Para o capacitor de ...
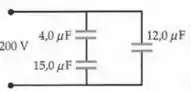
Passo 8
A energia armazenada em cada capacitor pode ser dada por...
Então...
Ou ainda...
Para o capacitor e tensão ...
Ou...
E para o capacitor ...
Ou...
Resposta
Letra A:
Letra B:
Letra C:
Letra D: