Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Tipler - Vol 2- Ed: 6º - Capítulo 24.1 - Ex. 34

Para o circuito mostrado na Figura 24-37 determine

  1. A capacitância equivalente entre os terminais.
  2. A carga armazenada na placa carregada positivamente de cada capacitor.
  3. A tensão em cada capacitor, e;
  4. A energia total armazenada.

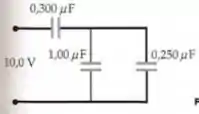
Passo 1

L e t r a   A :

Repare que podemos primeiro chegar na equivalência C p a r que é a equivalência somente para a parte paralela...

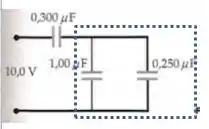
Essa capacitância paralela equivalente vai ser...

C p a r = 0,250 μ F + 1,00   μ F   →

C p a r = 1,250 μ F

Agora, para encontrar a capacitância equivalente do circuito todo, a gente tem que fazer a série entre a capacitância 0,300   μ F com a C p a r . Pelo nosso Bizu de se encontrar capacitância em série...

C e q = 0,300 μ F ⋅ 1,250 μ F 0,300 μ F + 1,250 μ F   →

C e q = 0,375 μ 2 F 2 1,550 μ F   →

C e q = 0,242   μ F

Então essa é a capacitância equivalente do circuito inteiro .

Passo 2

L e t r a   B :

Como o capacitor de 0,300 μ F está em série com o capacitor C p a r , podemos afirmar que as suas cargas tem que ser a mesma...

Q p a r = Q 0,3

A carga do capacitor 0,300 é...

C p a r V p a r = 0,300 μ ⋅ V 0,3 →

1,250   μ ⋅ V p a r = 0,300 μ ⋅ V 0,3

E sabemos que a soma das duas tensões, deve ser igual a tensão total da fonte...

V p a r + V 0,3 = 10 V

Então, isolando V 0,3 (tensão em cima do capacitor 0,300 μ F ) e substituindo na equação de cima...

V 0,3 = 10 - V p a r         →             1,250   μ ⋅ V p a r = 0,300 μ ⋅ V 0,3     →

  1,250   μ ⋅ V p a r = 0,300 μ ⋅ 10 - V p a r →

  1,250   V p a r = 0,300 10 - V p a r →

1,250   V p a r = 3 - 0,3 V p a r →

1,250   V p a r + 0,3 V p a r = 3 →

1 , 5 50   V p a r = 3 →

V p a r = 1,94   V

Então...

V 0,3 = 8,06   V

Com essas tensões podemos determinar as cargas em cada capacitor...

Q 0,3 = C 0,3 V 0,3     →

Q 0,3 = 0,300 μ F ⋅ 8,0 6     →

Q 0,3 = 2,418 μ C

E para as cargas em cima dos capacitores que estão em paralelos...

Q 1 = 1,00   μ F ⋅ V p a r           e             Q 2 = 0,250 μ F ⋅ V p a r   →

Q 1 = 1,00   μ F ⋅ 1,9 4             e             Q 2 = 0,250 μ F ⋅ 1,9 4     →

Q 1 = 1,9 4   μ C             e             Q 2 = 0,48 5 μ C

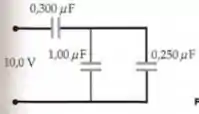
Passo 3

L e t r a   C :

Já fizemos esse item no item anterior, neh? Então só vou coloca-los aqui...

V 0,3 = 8,06   V

V 1 = 1,94   V

V 2 = 1,94   V

Passo 4

L e t r a   D :

A energia total armazenada vai ser...

U = 1 2 C e q V 2

Onde V é a tensão em cima dos três capacitores cuja capacitância equivalente é...

C e q = 0,242   μ F   →

Então…

U = 1 2 0,242   μ 10 2   →

U = 12,1   μ J

Resposta

Letra A:

C e q = 0,242   μ F

Letra B:

Q 0,3 = 2,418 μ C

Q 1 = 1,9 4   μ C             e             Q 2 = 0,485 μ C

Letra C:

V 0,3 = 8,06   V

V 1 = 1,94   V

V 2 = 1,94   V

Letra D:

U = 12,1   μ J

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A vida média de um núcleo radioativo é τ . Quanto vale t 2 - ?
Um bêbado anda em passeio aleatório, com passos de 70 c m , e o comprimento total de sua trajetória é 5,0 k m . Calcule o valor r r m s de sua posição final.
O tempo médio de voo livre dos elétrons em um dado sólido é τ = 5,0 ⋅ 10 - 12s . Qual é a velocidade de arraste dos elétrons quando o material está sob um campo elétrico de intensidade 0,10V / m ?
A meia-vida do isótopo C o 57 é de 245 dias. Uma fonte radioativa desse isótopo apresenta uma atividade de 0,100 curie, ou seja, 3,70 ⋅ 10 9 desintegrações por segundo. Quantos átomos de C o 57 existe
Considere bolas de sinuca de raio R , dispersadas de forma aleatória sobre a mesa, com densidade (bolas por unidade de área) σ . Mostre que o livre percurso médio de uma bola adicional posta a rola so