Enunciado
Física - Tipler - Vol 2- Ed: 6º - Capítulo 25.1 - Ex. 104
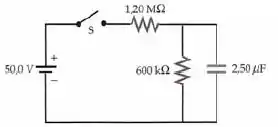
Para o circuito mostrado na figura abaixo, a chave S permaneceu aberta por um longo tempo. No instante a chave é, então, fechada. (a) Qual é a corrente na bateria logo após a chave S ter sido fechada? (b) Qual é a corrente na bateria um longo tempo depois da chave S ter sido fechada? (c) A chave permaneceu fechada por um longo tempo. No tempo a chave é, então, aberta. Determine a corrente no resistor de como função do tempo.
Passo 1
EAE GALERA! Vamos matar essa a paulada! BIRLL! Adotaremos para representar o resistor de e para representar o resistor de . Existem três possíveis cenários para esse circuito:
1) Imediatamente depois que a chave é fechada, o capacitor possui carga igual a zero e a diferença de potencial entre ele também é zero;
2) Um longo tempo depois que a chave é fechada, o capacitor estará totalmente carregado e a diferença de potencial entre ele será dado por ou ;
3) Quando a chave é aberta depois de estar fechada por um longo período de tempo, tanto o resistor quanto a fonte de tensão estarão fora do circuito e o capacitor totalmente carregado irá descarregar através de ;
Poderíamos utilizar a Segunda Lei de Kirchhoff’s para encontrar as correntes no circuito quando a chave é imediatamente fechada, quando a chave é fechada por um longo período de tempo e quando a chave é aberta após ter passado por um longo período de tempo fechada.
DITO ISTO, VAMOS PARA A RESOLUÇÃO (hora dos cálculos, baby)
Passo 2
Começaremos aplicando a Segunda Lei de Kirchhoff’s no circuito considerando o cenário de número 1, para obtermos a resposta da alternativa (a):
Como , temos:
Substituindo pelos valores numéricos dados na questão, temos:
Terminamos essa alternativa, vamos para a próxima!
Passo 3
Aplicando a Segunda Lei de Kirchhoff’s no circuito considerando o cenário de número 2, para obtermos a resposta da alternativa (b):
Substituindo pelos valores numéricos dados na questão, temos:
Terminamos mais uma alternativa! Vamos para a última!
Passo 4
Aplicando a Segunda Lei de Kirchhoff’s no circuito considerando o cenário de número 3, para obtermos a resposta da alternativa (c):
Sabemos que , substituindo:
Onde substituindo pelos valores numéricos, temos que:
PRONTO, foram todas as alternativas! Até a próxima galera.
Resposta
a)
b)
c)