Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Tipler - Vol 2- Ed: 6º - Capítulo 25.1 - Ex. 103

Para o circuito mostrado na figura abaixo, a chave S permaneceu aberta por um longo tempo. No instante t = 0 , a chave é, então, fechada. (a) Qual é a corrente na bateria logo após a chave S ter sido fechada? (b) Qual é a corrente na bateria um longo tempo depois de a chave S ter sido fechada? (c) Qual é a corrente no resistor de 600   Ω como função do tempo?

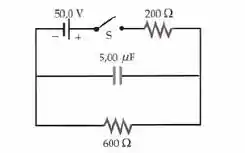
Passo 1

OPA, fala a boa, meu consagrado, antes de iniciarmos o raciocínio que utilizaremos, vamos considerar R 1 = 200 Ω ,   R 2 = 600 Ω , I 1 e I 2 seriam as suas correntes, e I 3 seria a corrente no capacitor. Para obtermos a corrente inicial I 0 e a corrente após um longo tempo após a chave ser fechada I ∞ basta aplicar a Segunda Lei de Kirchhoff’s. Para a parte (c) podemos aplicar a primeira e a segunda Lei de Kirchhoff’s para obtermos equações diferenciais lineares com coeficientes constantes, descrevendo a corrente no resistor de 600   Ω como uma função do tempo. Podemos solucionar essa equação diferencial assumindo uma solução e depois diferenciando essa solução e substituindo sua derivada na equação diferencial. Igualar os coeficientes requer uma solução que seja valida para todos os valores das constantes assumidas, e determinar uma condição inicial nos permitirá que achemos as constantes na solução estabelecida. Dito isto, vamos partir para as alternativas!

Passo 2

Começaremos pela alternativa (a), aplicando a Segunda Lei de Kirchhoff’s no circuito quando a chave for instantaneamente fechada:

ℇ - 200   Ω I 0 -   V C 0 = 0

Já que o capacitor está inicialmente descarregado, temos V C 0 = 0 , logo:

ℇ - 200   Ω I 0 = 0

- 200   Ω I 0 = - ℇ

I 0 = ℇ 200   Ω

I 0 = 50.0   V 200   Ω

I 0 = 0.250   A

Agora para a letra (b) faremos o mesmo processo, com a exceção que será no período em que a chave foi fechada por muito tempo:

ℇ - 200   Ω I ∞ -   600 Ω I ∞ = 0

- 200   Ω I ∞ -   600 Ω I ∞ = -   ℇ

I ∞ ( 200   Ω +   600 Ω ) =   ℇ

I ∞ = ℇ 200   Ω +   600 Ω

I ∞ = 50.0   V   800   Ω

I ∞ = 62.5   m A

Terminado as partes (a) e (b), vamos agora para a mais complicadinha, A GENTE TIRA DE LETRA, let’s goooo!

Passo 3

Aplicando a Primeira Lei de Kirchhoff’s nos pontos entre o resistor de 200   Ω e o capacitor para obter:

I 1 =   I 2 +   I 3 (1)

Agora, vamos aplicar a Segunda Lei de Kirchhoff’s na malha contendo a fonte, o resistor de 200   Ω e o capacitor, para obter:

ℇ -   R 1 I 1 - Q C = 0 (2)

Agora, vamos aplicar a Segunda Lei de Kirchhoff’s na malha contendo o resistor de 600   Ω e o capacitor, para obter:

Q C -   R 2 I 2 = 0 (3)

Diferenciando a equação (2) em relação ao tempo, temos:

d d t ℇ -   R 1 I 1 - Q C = 0

0 - R 1 d I 1 d t - 1 C d Q d t = 0

- R 1 d I 1 d t - 1 C I 3 = 0

R 1 d I 1 d t = - 1 C I 3 (4)

Diferenciando a equação (3) em relação ao tempo, temos:

d d t Q C -   R 2 I 2 = 0

1 C I 3 - R 2 d I 2 d t = 0

- R 2 d I 2 d t = -   1 C I 3

R 2 d I 2 d t =   1 C I 3 (5)

Usando a equação (1), substituiremos I 3 na equação (5), para obter:

R 2 d I 2 d t =   1 C ( I 1 - I 2 )

d I 2 d t =   1 R 2   C ( I 1 - I 2 ) (6)

Resolvendo a equação (2) para I 1 :

-   R 1 I 1 = - ℇ + Q C

  I 1 = ℇ - Q C R 1

I 1 = ℇ - R 2 I 2 R 1

Substituindo I 1 na equação (6) e simplificando para obter uma equação diferencial para I 2 :

d I 2 d t =   1 R 2   C ( I 1 - I 2 )

d I 2 d t =   1 R 2   C ℇ - R 2 I 2 R 1 - I 2

d I 2 d t =   ℇ R 1 R 2   C - R 1 + R 2 R 1 R 2   C I 2 (7)

Para resolvermos essa equação diferencial podemos assumir uma solução na forma:

I 2 t =   a + b   e - t / τ (8)

Diferenciando a equação (8) e igualando com a equação (7), obtemos:

- b τ e - t / τ =   ℇ R 1 R 2   C - R 1 + R 2 R 1 R 2   C I 2    

Igualando os coeficientes de e - t / τ , obtemos:

τ =   R 1 R 2   C R 1 + R 2

Precisamos de uma equação que seja valida para todos os valores que a pode assumir:

a = ℇ R 1 + R 2  

Se I 2 precisa ser zero quando t = 0 , então:

0 = a + b

b = - a

b = - ℇ R 1 + R 2

Substituindo isso na equação 8, temos que:

I 2 t =   ℇ R 1 + R 2 - ℇ R 1 + R 2   e - t / τ

I 2 t = ℇ R 1 + R 2 ( 1 - e - t / τ )    

Onde:

τ =   R 1 R 2   C R 1 + R 2

τ =   200   Ω 600   Ω 5.00   μ F 200   Ω + ( 600   Ω )

τ =   0.750   m s

Substituindo as variáveis de I 2 ( t ) pelos valores obtidos:

I 2 t = 50.0   V 200   Ω + 600   Ω ( 1 - e - t / 0.750   m s )  

I 2 t = ( 62.5   m A ) ( 1 - e - t / 0.750   m s )    

PRONTO, resolvemos tudo, até a próximaaa.

Resposta

a) I 0 = 0.250   A

b) I ∞ = 62.5   m A

c) I 2 t = ( 62.5   m A ) ( 1 - e - t / 0.750   m s )    

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

No circuito da Figura abaixo, C = 0 ,120μ F e ℇ = 100 Vℇ . A chave é girada para o contato b depois de ter estado no contato a por um longo tempo, e 4.00 s depois, a diferença de potencial no capacito
Para o circuito mostrado na Figura abaixo, C = 6,00μ F , ℇ = 100 Vℇ e R = 500 Ω . Depois de ter estado em contato com a por um longo tempo, o interruptor é girado para o contato com b. (a) Qual é a ca
No circuito da figura abaixo, a fem é igual a 6,00 V e a resistência interna é desprezível. A capacitância é igual a 1,50μ F e a resistência é igual a 2,00M Ω . A chave S ficou fechada por um longo te
No circuito da Figura abaixo, a fem é igual a 50.0V e a capacitância é igual a 2.00μ F . A chave S é aberta depois de permanecer fechada por um longo tempo, e 4.00 s depois, a queda de tensão no resis