Enunciado
Física - Tipler - Vol 2- Ed: 6º - Capítulo 25.1 - Ex. 88
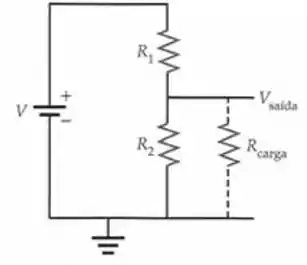
O fragmento de circuito mostrado na Figura 25-64 é chamado de divisor de tensão. (a) Se Rload não estiver conectado, mostre que Vout = VR2 / (R1 + R2). (b) Se R1 = R2 = 10 kΩ, qual é o menor valor de Rload que pode ser usado para que Vout caia menos de 10 por cento de seu valor descarregado? (Vout é medido em relação ao solo.
Passo 1
Eae galera! Tudo tranquilo? Tendo uma visão geral da coisa, deixe a corrente retirada da fonte ser I. Podemos usar a lei de Ohm em conjunto com a regra de loop de Kirchhoff para expressar a tensão de saída como uma função de V, R1 e R2.
Passo 2
Vamo lá. Usando a lei de Ohm para expressar em temos de R2 e I:
Aplique a regra de loop de Kirchhoff ao circuito para obter:
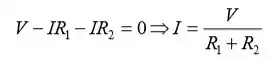
Substituindo I por Vout, temos:
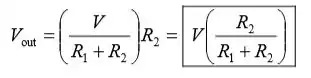
No item (b), Relacione a resistência efetiva do circuito carregado Reff com R2 e Rload:
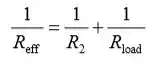
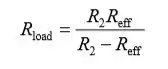
Deixando sair V’ representar a tensão de saída sob carga, expressa a condição de que V fora cai menos de 10 por cento de seu valor descarregado:
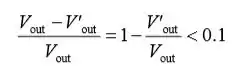
Passo 3
Belezinha, vamos lá. Usando o resultado de (a), expresse Vout’ termos da carga de saída efetiva Reff:
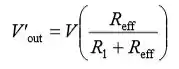
Substitua para fora V e fora V 'na equação (2) e simplifique para obter:
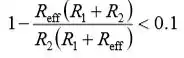
Isolando Reff,
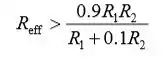
Substitua os valores numéricos e avalie o Reff:
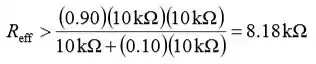
Logo,
