Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 19.1 - Ex. 82

Compare o rendimento do ciclo Otto com o rendimento do ciclo de Carnot operando entre as mesmas temperaturas máxima e mínima. (O ciclo Otto é discutido na Seção 19-1).

Passo 1

Muito bem, o rendimento do ciclo de Otto é fornecido pra gente, certo?

ε = 1 - T d - T a T c - T b

De acordo com a figura:

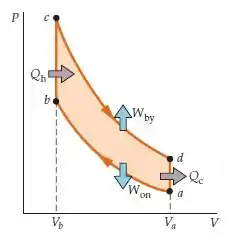
Vamos precisar achar uma relação entre estas temperaturas para que a gente possa manipular a equação.

Sabendo que o segmento ab e cd são adiabáticos:

T a . V a γ - 1 = T b . V b γ - 1

Isolando T b :

T b = T a V a V b γ - 1

Para o outro segmento:

T c . V c γ - 1 = T d . V d γ - 1

Isolando T b :

T c = T d V d V c γ - 1

Na equação do rendimento:

ε = 1 - T d - T a T d V d V c γ - 1 - T a V a V b γ - 1

Lembrando que:

V d = V a

V c = V b

Substituindo:

ε = 1 - T d - T a T d V a V b γ - 1 - T a V a V b γ - 1 = 1 - T d - T a ( T d - T a ) V a V b γ - 1

Então:

ε = 1 - 1 V a V b γ - 1

Reorganizando:

ε = 1 - V b V a γ - 1

Lembrando da relação válida para processos adiabáticos:

T b . V b γ - 1 = T a . V a γ - 1

Isolando V b V a γ - 1 :

V b V a γ - 1 = T a T b

Na eficiência:

ε = 1 - T a T b

Passo 2

Vamos analisar qual das temperaturas é máxima ou mínima. Considerando os processos à volume constante, ad e bc.

Para gases ideais:

P V = n R T

Então o termo n R V é constante:

P a T a = P d T d → T d = T a P d P a  

Então:

T d > T a

Para o segmento bc:

P b T b = P c T c → T c = T b P c P d  

Então:

T c > T b

Sendo assim, temos que T a é a temperatura mínima do ciclo, e T c a temperatura máxima.

Para um ciclo de Carnot:

ε c = 1 - T a T c  

Relacionando ambas as eficiências:

ε ε c = 1 - T a T b   1 - T a T c    

Como T c > T b

Então:

T a T c   < T a T b  

Concluindo que:

1 - T a T c   > 1 - T a T b  

Ou seja,

ε c > ε

Resposta

ε c > ε

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um dispositivo de Carnot extrai 5,0k J de calor de um corpo a - 10° C . Que trabalho é realizado quando o dispositivo rejeita calor para o ambiente a uma temperatura de a) 25° C ; b) 0° C ; c) - 25° C
Uma máquina ideal de Carnot funciona entre 500° C e 100° C com um fornecimento de calor de 250J por ciclo. a) Que quantidade de calor é fornecida ao reservatório frio em cada ciclo? b) Qual é o número
Uma máquina de Carnot tem uma eficiência de 59 % e realiza 2,5 × 10 4J de trabalho em cada ciclo. a) Quanto calor a máquina extrai de sua fonte de calor e cada ciclo? b) Suponha que a máquina rejeite
Uma máquina que produz gelo opera com um ciclo de Carnot. Ela recebe calor da água a 0° C e rejeita calor para uma sala a 24° C . Suponha que 85,0k g de água a 0° C sejam convertidos em gelo a 0° C .
Um refrigerador de Carnot opera entre dois reservatórios de temperaturas 320K e 270K . a) Se em cada ciclo o refrigerador recebe 415J de calor do reservatório a 270K , qual é a quantidade de calor em