Enunciado
Física - Halliday - Vol 4- Ed: 10º - Capítulo 33.Problemas Adicionais - Ex. 105
A componente magnética de uma onda polarizada é dada por Determine (a) a direção de propagação da onda, (b) a direção de polarização da luz e (c) a intensidade da onda. (d) Escreva uma expressão para o campo elétrico da onda, incluindo o valor do número de onda. (e) Determine o comprimento de onda. (f) A que parte do espectro eletromagnético pertence a onda?
Passo 1
E aí meus caros(as)! Bora agora pra questão 105!
No primeiro item, a gente tem que descobrir a direção de propagação da onda!
a) Bom! A gente sabe que a componente magnética da onda é dada por...
Isso vai nos fornecer uma onda que está se propagando no sentido do semieixo negativo.
Podemos observar isso, remetendo ao módulo 16-1 do Halliday, através do sinal que precede a parte temporal da função de onda e o sentido de propagação da onda. Um sinal positivo para uma onda que depende de , indica que o sentido vai ser o do semieixo negativo correspondente.
Passo 2
b) Para esse segundo item, em que temos que descobrir a direção de polarização da luz, vamos dar uma olhada na figura abaixo...
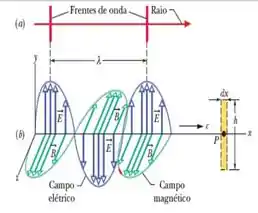
A direção de propagação (ao longo do eixo ) é perpendicular a (que aponta na direção do eixo , já que a única componente do campo magnético é ), e o campo é perpendicular às duas .
Isso vai nos dar uma onda que está polarizada na direção do eixo !
Passo 3
c) Continuando nossa batalha, agora vamos descobrir a intensidade da onda.
E pra fazer isso, temos que recorrer à equação abaixo...
Para descobrir , antes é preciso saber que ele se relaciona com o campo elétrico da seguinte forma:
Desse modo, podemos obtê-lo através da equação abaixo...
Substituindo e isolando:
Como :
Assim, a intensidade, dado que ; será de:
Passo 4
d) Em seguida, a gente vai tratar de obter uma expressão para o campo elétrico da onda, que está no eixo e é dado por...
Bem! Tá faltando obter o valor de !
Molezinha! Ele é dado pela equação abaixo...
Como :
Ficamos assim, com a seguinte expressão:
Passo 5
e) A missão agora é obter o comprimento de onda!
Ora bolas! Não seja por isso!
Basta usar a equação abaixo:
Onde, substituindo os valores numéricos:
f) E pela tabela de comprimento de onda, podemos ver que essa onda está na faixa do infravermelho!
Resposta
a)
b)
c)
d)
e)
f)
da relação entre
Resposta
a)
b)
c)
d)