Enunciado
Física - Halliday - Vol 4- Ed: 10º - Capítulo 33.Problemas Adicionais - Ex. 104
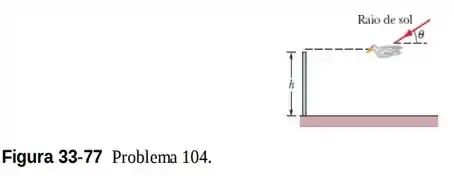
Na Fig. 33-77, um albatroz está planando horizontalmente com uma velocidade constante de acima de um terreno plano, movendo-se em um plano vertical que inclui o Sol. A ave se aproxima de uma parede de altura e está à mesma altura do solo que a extremidade superior da parede. Nessa hora do dia, o ângulo do Sol em relação ao solo é . Com que velocidade a sombra do albatroz se move (a) horizontalmente, ao longo do solo, e (b) verticalmente, ao longo da parede? Mais tarde, um gavião percorre o mesmo caminho, com a mesma velocidade. Você observa que, no momento em que a sombra do gavião atinge a parede, a velocidade da sombra aumenta perceptivelmente. (c) Nesse momento, o Sol está mais alto ou mais baixo no céu que durante o voo do albatroz? (d) Se a velocidade da sombra do gavião na parede é , qual é o ângulo do Sol nesse momento?
Passo 1
E aí meus caros(as)! Bora agora pra questão 104!
No primeiro item, a gente tem que descobrir a velocidade que a sombra do albatroz está se movendo!
a) Agora se liga! A gente tem a seguinte imagem abaixo, que esboça mais ou menos como os raios de sol incidem no passarinho...
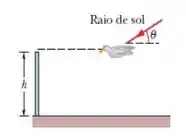
Acontece que a gente tem que considerar que o sol está suficientemente distante da Terra para que os raios solares sejam considerados paralelos.
Em
Desse modo, se um raio solar faz um ângulo com a horizontal quando o pássaro está em uma posição, outro raio faz o mesmo ângulo com a horizontal quando o pássaro está em outra posição.
E então, a sombra do albatroz vai se mover à mesma velocidade que o pássaro, isto é...
Passo 2
b) Agora, vamos ter de obter a velocidade do albatroz, verticalmente ao longo do parede.
Para isso, vamos dar uma olhada na seguinte figura abaixo...
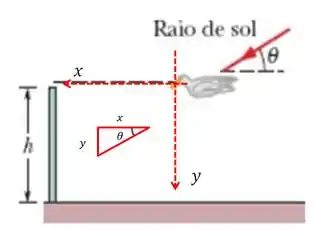
Pela imagem acima, podemos ver...
Como o pássaro, e consequentemente sua sobra, mudam de posição conforme o tempo, vamos derivar os dois lados da equação acima em relação à :
é a velocidade da sombra do albatroz na horizontal, que no item anterior, descobrimos ser igual à:
E como a questão nos fornece o ângulo de ...
Como adotamos o eixo positivo para baixo, isso significa que a distância (medida como uma distância positiva para baixo a partir do alto da parede) está diminuindo à taxa de .
Passo 3
c) Vamos analisar agora, a posição do Sol durante o voo do albatroz comparando com o do gavião.
Bom! Anteriormente a gente descobriu a seguinte fórmula para o voo desses pássaros aí:
Quando o ângulo aumenta a partir de , já que o seno está aumentando e o cosseno diminuindo, significa que um valor maior de está associado a um valor maior de .
Logo, o Sol vai estar mais alto no céu durante o voo do gavião do que durante o voo do albatroz... Já que por sua velocidade da sombra na parede ser maior, o ângulo também será!
Passo 4
d) A mesma fórmula que vale para o albatroz, vale também para o gavião...
Vamos isolar , que é o que pede esse item:
E a questão nos diz que a velocidade da sombra do gavião na parede é . Isto é...
Só que quando a velocidade horizontal da sombra do gavião, conforme fala o enunciado, vai ser a mesma do albatroz...
Assim, o ângulo será de...
Pronto! Obtivemos todas as nossas respostas!
Resposta
a)
b)
c)
d)