A componente do vetor é e a componente é . (a) Qual é o módulo de ?(b) Qual é o ângulo entre a orientação de e o semieixo positivo?
Passo 1
Nesta questão nós temos as componentes do vetor :
Ilustrando essas componentes no plano cartesiano:

Passo 2
Para calcular o módulo do vamos inicialmente desenhar um triângulo retângulo:
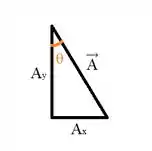
Como sabemos o valor dos componentes, podemos aplicar o teorema de Pitágoras para determinar o módulo de :
Passo 3
Com a mesma ilustração do passo anterior podemos encontrar o ângulo do com o semieixo positivo de usando relação trigonométrica. Para isso, usaremos a definição de cosseno :
Determinando :
Como o enunciado pediu o ângulo que o vetor faz com o semieixo positivo de , somamos ao ângulo encontrado acima.