Na figura abaixo, mostra as partículas 1 e 2, ambas de massa m, presas às extremidades de uma barra rígida de massa desprezível e comprimento L1 + L2, com L1=20 cm L2= 80 cm. A barra é mantida horizontalmente no fulcro até ser liberada. Qual é o módulo da aceleração inicial (a) da partícula 1 e (b) da partícula 2?
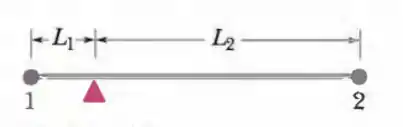
Passo 1
Bora resolver essa?
Aqui queremos encontrar a aceleração do corpo 1.
Para isso, iremos encontrar a aceleração angular desse sistema. Essa aceleração angular, vem da expressão:
Aonde é o momento de inércia do sistema e será dado por:
E é o torque resultante sobre esse sistema. Vamos encontra-lo!
Passo 2
Para começar, vamos fazer um diagrama da forças...
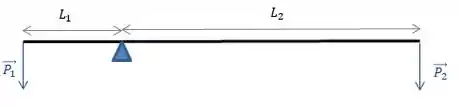
Considerando que o sentido anti-horário (por convenção) será o nosso positivo, temos que o torque gerado por será positivo e o gerado por será negativo, como na imagem:
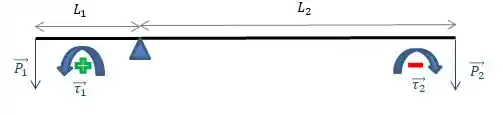
Sendo assim, vamos calcular esses torques:
E como
Passo 3
Agora que temos o nosso torque resultante, podemos encontrar a nossa aceleração angular...
Substituindo o que temos:
Usando a gravidade como 9,8...
Nossa aceleração angular deu negativa, o que índica para a gente que o nosso sistema começa a girar no sentido horário... Com isso, podemos encontrar o sentido da aceleração tanto do objeto 1 quanto do objeto 2:
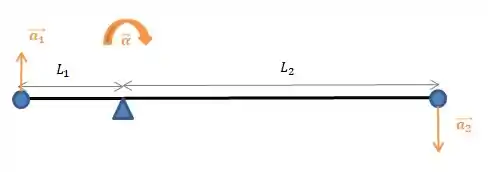
Agora, para responder a letra dessa questão, só precisamos usar a relação:
A questão apenas pediu o módulo, mas se quisesse, você ainda pode mostrar que é braba(o) e indicar que essa aceleração aponta pra cima!
Resposta
a)