Enunciado
Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 27.Exercício - Ex. 9
9- Um conjunto de partículas percorre um campo magnético de módulo, direção e sentido desconhecidos. Você observa que um próton se movendo a no sentido sofre uma força igual a na direção , e um elétron que se move a na direção sofre uma força de .
Quais são o módulo, a direção e o sentido do campo magnético?
Quais são o módulo, a direção e o sentido da força magnética sobre um elétron que se move no sentido a ?
Passo 1
A força magnética nas duas partículas serão dadas pela equação vetorial abaixo:
Então sabendo que a carga elementar é de nós temos que a equação no próton será igual a:
Nessa equação vemos que que tem sentido em para que tenhamos sentido positivo em . E que valerá:
Passo 2
Já no elétron temos que:
E como do passo anterior não temos nenhum campo em , e encontramos um campo em , logo a única parcela que vai gerar força nessa partícula é um campo em (estando no eixo positivo ou negativo já que não se fala do sentido dessa força), logo:
Então o vetor componente será de:
Cuja intensidade será de:
E ainda podemos ir mais além, o ângulo formado entre os eixos e é dado por:
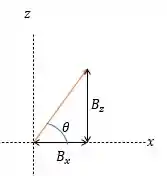
Passo 3
Com esse campo que calculamos temos agora um outro elétron com
Então a força magnética será de:
Então sabendo das regras de multiplicação vetorial abaixo.
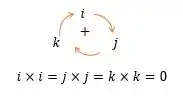
Nós temos que:
O que nos dá:
Cujo módulo dessa força será:
E o ângulo formando entre os eixos e será de:
Que é o complemento em relação ao campo magnético.