Enunciado
Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 23.Exercício - Ex. 24
Considere o arranjo de cargas. Umas carga positiva está localizada no ponto e e uma carga negativa está localizada no ponto e . a)Deduza uma relação para o potencial em qualquer ponto sobre o eixo em função da coordenada .Considere zero o potencial a uma distância infinita das cargas. b)Faça um gráfico do potencial sobre o eixo em função de de até . c)Mostre que, quando , o potencial em qualquer ponto sobre a parte positiva do eixo é dado por . d)Qual seria a resposta dos itens (b) e (c) se as cargas trocassem de posição, ou seja, se fosse localizada em r em ?
Passo 1
letra a)
O potencial elétrico é dado por:
O potencial total em qualquer ponto é a soma dos potenciais das duas cargas.
Precisamos agora encontrar quem são as distâncias.
Passo 2
Considere as distâncias do ponto no eixo a cada carga para as três regiões:
(entre as duas cargas), (acima de ambas as cargas) e (abaixo de ambas as cargas).
Passo 3
Para a região :
O potencial será:
Passo 4
Para a região :
O potencial será:
Passo 5
Para a região :
O potencial será:
Passo 6
letra b)
Como temos três regiões para o potencial, então nosso gráfico teŕa três regiões.
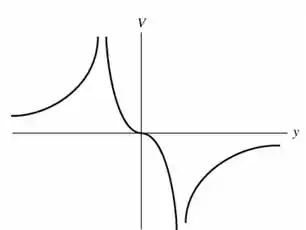
Passo 7
letra c)
Quando ,
Passo 8
letra d)
Se as cargas forem trocadas, o potencial terá o sinal oposto.
Resposta
letra a),
,
,
letra b)
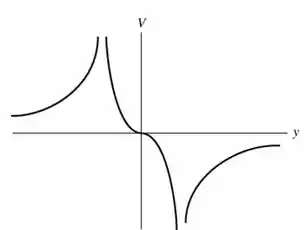
letra d)potencial terá o sinal oposto