Considere o caminho de uma partícula em movimento. (a) como o vetor velocidade se relaciona geometricamente ao caminho tomado pela partícula? (b) esboce um caminho curvado e desenhe o vetor da velocidade para várias posições ao longo do caminho.
Passo 1
(a) O vetor velocidade sempre aponta na direção tangente à trajetória da partícula. A melhor forma de mostrar isso é pensar na definição da velocidade:
Ou seja, a velocidade é a derivada da função da posição. Quando calcularmos a derivada de um vetor (afinal é um vetor), nós sempre encontramos um outro vetor que aponta na direção em que o primeiro está mudando.
Como é justamente a função que dá a trajetória da partícual, vai sempre apontar na direção em que a trajetória está mudando.
Passo 2
(b) Podemos representar isso em um desenho imaginando o lançamento de uma bola com um certo ângulo a partir da horizontal:
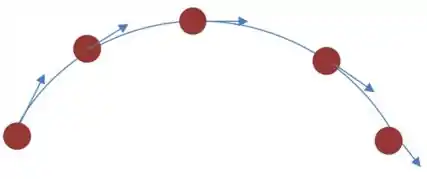
Resposta
(a) É um vetor tangente à trajetória da partícula.
(b) Ver desenho.