Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 4.Exercícios e Problemas - Ex. 1
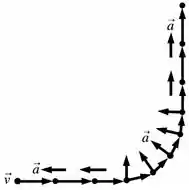
1.Os problemas de 1 a 3 mostram um diagrama de movimento incompleto. Em cada um deles:
Complete o diagrama de movimento acrescentando a eles vetores velocidade.
Redija um problema de física para o qual este seja um diagrama de movimento correto. Seja criativo! Não esqueça de incluir informação suficiente para que o problema seja completo e estabeleça claramente o que deve ser determinado.
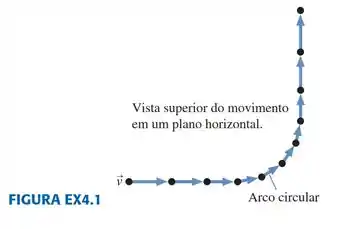
Passo 1
Essa questão tem um erro de tradução, no item onde tem “vetores velocidade”, o correto seria “vetores aceleração”. Veja que na própria já temos os vetores velocidade, não seria necessário encontra-lo novamente. Vc pode consultar a versão original do livro também. Nós iremos aplicar essa correção.
Passo 2
Diante da informação do , precisamos agora lembrar que em cinemática temos três itens fundamentais: posição, velocidade e aceleração. Todos esses se relacionam entre si.
Em resumo temos a posição como uma função originária, a velocidade como a primeira derivada dessa função posição, e a aceleração como a segunda derivada dessa função posição. É como se fosse mãe(posição), filha(velocidade) e neta(aceleração).
Mas como são grandezas vetoriais, precisamos saber como matematicamente elas aparecem no espaço, no seu livro texto vc pode ver com propriedade, mas para entender de forma resumida e direta, observe essa imagem a seguir, nela vc tem os vetores para cada item.
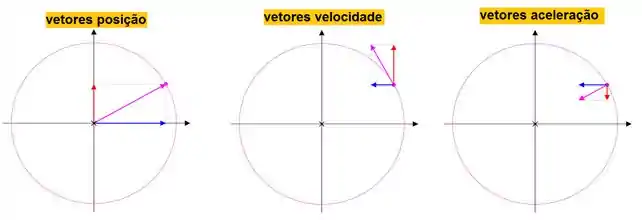
Nesse exemplo estamos mostrando uma trajetória circular, mas vc pode expandir o raciocínio para outras trajetórias. Veja como o vetor resultante (violeta), é decomposto em dois componentes retangulares x (azul) e y (vermelho). Perceba que todos estão representados em um mesmo ponto, mas mesmo assim os vetores são diferentes para cada item (posição, velocidade e aceleração).
Agora astuciosamente vamos por todos os vetores juntos, cuidado para não os confundir.
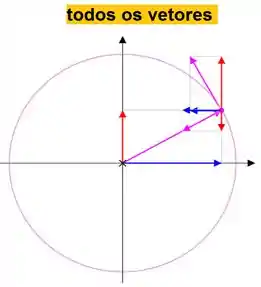
Agora com um pouquinho de esforço podemos ir para letra a...
Passo 3
(a)
Quando trabalhamos com velocidade e aceleração, temos que saber que, se o móvel está reduzindo sua velocidade a aceleração tem sentido oposto a essa velocidade. (é difícil de aceitar, mas é verdade.) assim, como na trajetória do exemplo o móvel reduz a velocidade para depois entrar na curva os vetores aceleração será assim expresso:
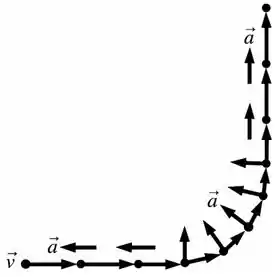
Veja,
-Ao reduzir a velocidade antes de entrar na curva:tem sentido oposto a
-Na curva:tem sentido para o centro e é tangencial (como nas imagens do )
-Ao aumentar a velocidade depois de sair da curva: :tem sentido igual a
Passo 4
Essa é uma questão bem aberta, vamos fórmular um problema de exemplo:
Um estudante segue numa pista reta e reduz a velocidade antes de entrar numa curva que lhe colocará a 90° anti-horário da pista que ele vem seguindo. Ele conhece a função velocidade que o carro descreve. Nessa situação o que ele deve fazer para saber sua aceleração num instante qualquer? Marque uma escolha correta, para o estudante:
( )Integrar a função velocidade conhecida por ele, e aplicar o instante qualquer.
( )Derivar a função velocidade conhecida por ele, e aplicar o instante qualquer.
Resposta
Para o problema desenvolvido, a resposta correta seria:
( x )Derivar a função velocidade conhecida por ele, e aplicar o instante qualquer.