Enunciado
Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 26.Problemas - Ex. 66
66- Considere o circuito indicado na Figura :
Qual deve ser a fem da bateria para que uma corrente de passe pela bateria de , conforme indicado? A polaridade da bateria está correta conforme indicado?
Quanto tempo leva para de energia termal ser produzida no resistor de ?
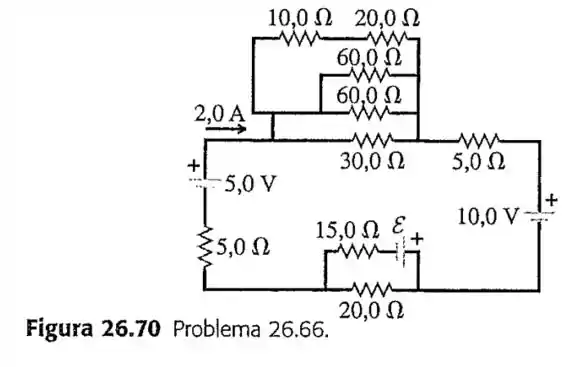
Passo 1
Primeiramente vamos transformar essa maçaroca de resistores da parte de cima do circuito em uma coisa só.
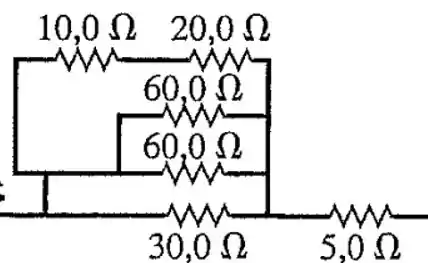
Tal como os dois resistores de em paralelo vira um resistor de que por sua vez está em paralelo com o resistor de tanto em cima (em série um de e outro de ), quanto em baixo(e com o de baixo de também) , nos dando um resistor só de que em série com um resistor de nos dá um resistor todo no ramo de cima igual a . Deixando o circuito da seguinte forma:
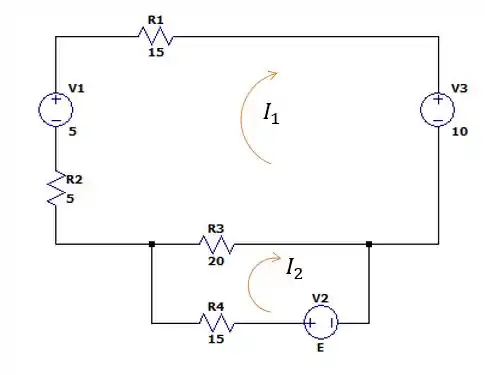
Passo 2
Uma vez que o circuito com a bateria de pode ser passada para baixo sem problema nenhum, e o lado bom é que foi nos dado e ele vale
Fazendo a somatória das tensões na primeira malha nós podemos encontrar o valor de que será:
E a somatória das tensões na segunda malha nos dá a tensão e que será:
Então a fem da bateria deve ser de e o sinal contrário nos indica que a polaridade está ao contrário.
Passo 3
Não sei se ficou claro a maçaroca de resistores que fizemos no passo 1, mas no final das contas é como se tivéssemos:
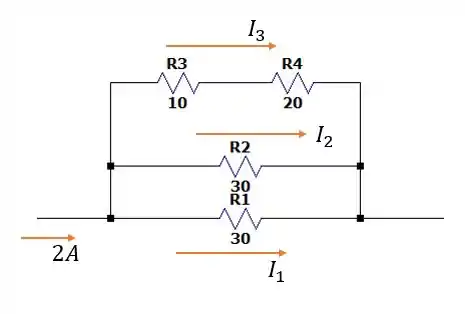
E como as resistências nos três ramos são iguais então podemos dizer que as correntes e são iguais e valem:
Portanto a potência no resistor de será de:
E o tempo necessário para termos de energia nesse resistor será: