Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 27.Problemas Adicionais - Ex. 82

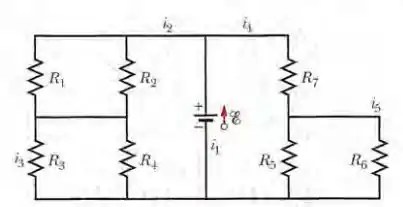
Na Fig. 27-70, a força eletromotriz da fonte ideal é ε = 30,0 V e as resistências são R 1 = R 2 = 14 Ω , R 3 = R 4 = R 5 = 6,0 Ω , R 6 = 2,0 Ω e R 7 = 1,5 Ω . Determine (a) i 2 ; (b) i 4 ; (c) i 1 ; (d) i 3 ; (e) i 5 .

Passo 1

Aqui temos um circuito e temos que saber a corrente em cada ponto pedido.

Passo 2

(a)Para calcular a corrente i 2 temos que fazer o calculo da resistencia equivalente dos resistores R 1 , R 2 , R 3 e R 4 pois R 1 e R 2 esoa em paralelo e R 3 e R 4 estão em paralelo entre si, logo o calculo fica assim?

R e q = R 12 + R 34 = R 1 R 2 R 1 + R 2 + R 3 R 4 R 3 + R 4

substituindo os valores

R e q = 14 Ω × 14 Ω 14 Ω + 14 Ω + 6,0 Ω × 6,0 Ω 6,0 Ω + 6,0 Ω = 7,0 Ω + 3,0 Ω = 10,0 Ω

Como a fem da fonte está aplicada aos terminais de R e q , temos:

i 2 = ε R e q = 30,0 V 10,0 Ω = 3,0 A

Passo 3

(b) Agora a situação é que R 5 e R 6 estão em paralelo e R 7 está em série com esses dois logo, a resistência equivalente dos resistores R 5 , R 6 e R 7 é

R e q ‘ = R 56 + R 7 = R 5 R 6 R 5 + R 6 + R 7

substituindo os valores

R e q ‘ = 6 Ω × 2 Ω 6 Ω + 2 Ω + 1,5 Ω = 3,0 Ω

Como a fem da fonte está aplicada aos terminais de R e q ' , temos:

i 4 = ε R e q ‘ = 30,0 V 3,0 Ω = 10,0 A

Passo 4

(c) Aqui teremos que usar a regra dos nós,

i 1 = i 2 + i 4 = 3,0 A + 10,0 A = 13 A .

Passo 5

(d)Por simetria, pois i 3 só está conectado a metade das resistencias que i 2 , temos:

i 3 = i 2 2 = 1,5 A

Passo 6

(e)Aplicando a regra das malhas à malha que contém a fonte e os resistores R 6 e R 7 , temos

ε – i 4 R 7 – i 5 R 6 = 30 V – 10,0 A × 1,5 Ω – i 5 2,0 Ω = 0

i 5 = 7,5 A

Resposta

(a) i 2 = 3,0 A

(b) i 4 = 10,0 A

(c) i 1 = 13 A .

(d) i 3 = 1,5 A

(e) i 5 = 7,5 A

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

(a)Determine a resistencia equivalente entre os pontos a e b na figura 25.57. (b)Se a queda de potencial entre os pontos a e b é 12V , determine a corrente em cada resistor.
As baterias do circuito na figura 25-60 têm resistência interna desprezível. (a) Encontre a corrente usando a regra do loop de Kirchhoff. (b) Encontre a energia entregue ou fornecida por cada bateria.
Verifique seus resultados para o Problema 79 usando os seguintes valores específicos: (a) R1 = 4,00 Ω, R2 = 6,00 Ω; (b) R1 = 4,00 Ω, R3 = 3,00 Ω; e (c) R2 = 6,00 Ω, R3 = 3,00 Ω.
Na Figura 25-59, o emf da bateria é 6,00 V e R é 0,500 Ω. A taxa de aquecimento Joule em R é 8,00 W. (a) Qual é a corrente no circuito? (b) Qual é a diferença em potencial entre R? (c) Qual é a resist
Para a rede mostrada na Figura 25-58, deixe R a b denotar a resistência equivalente entre os terminais a e b. Find (a) R 3 , de modo que R a b = R 1 , (b) R 2 , de modo que R a b = R 3 ; e (c) R 1 , d