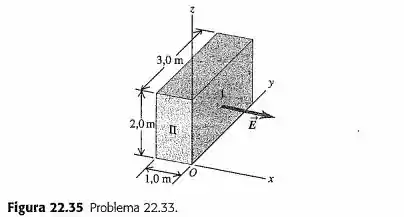
O campo elétrico na Figura é paralelo ao eixo em todos os pontos da região, portanto os componentes e são nulos. O componente do campo elétrico depende de , mas não depende de nem de . Sobre os pontos do plano (em que ), . Calcule o fluxo elétrico através da superfície na Figura . Qual é o fluxo elétrico através da superfície ? O volume indicado na figura é uma pequena seção de uma viga isolante muito grande, com espessura igual a . Sabendo que existe uma carga igual a no interior do volume indicado, determine o módulo, a direção e o sentido de sobre a face oposta à face . O campo elétrico existente é produzido somente pelas cargas no interior da viga ou pode ser produzido também por cargas existentes fora da viga? Como se pode ter certeza disso?

Para a superfície , podemos ver na figura que o vetor campo elétrico é perpendicular à essa superfície, o que faz com que o ângulo seja . Além disso, a sua área é:

Logo, o fluxo por essa superfície é:

Já para a superfície , o vetor campo elétrico é paralelo em relação a ela, o que faz com que o ângulo entre ambos seja . Logo, o fluxo elétrico é nulo.

A face oposta à superfície sofrerá efeito dos fluxos gerados pelo campo elétrico e pelo campo gerado pela carga interna. Assim, utilizando a lei de Gauss, teremos:

Onde e aponta para a face oposta a face , logo, aponta para o sentido negativo de . Então:

Portanto:

O campo elétrico existente não é formado apenas pelas cargas no interior da viga, pelo fato delas serem negativas, o que faria com que o campo elétrico apontasse para dentro da viga. No entanto, está indo em direção oposta a essa superfície, o que é causado por conta da presença de cargas externas que geram um campo elétrico externo que afeta o campo existente.