Considere o dipolo elétrico do Exemplo 21.15
(a) Deduza uma expressão para o módulo do campo elétrico produzido pelo dipolo em um ponto sobre o eixo da figura 21.34. Qual é a direção e o sentido desse campo elétrico?
(b) Como o campo elétrico nos pontos sobre o eixo depende de x quando este é muito grande?
Passo 1
(a) Temos que deduzir uma expressão para o campo elétrico de um dipolo. Um dipolo é composto por duas cargas de mesmo módulo, mas sinais opostos. Bom, nossa situação é basicamente essa aqui:
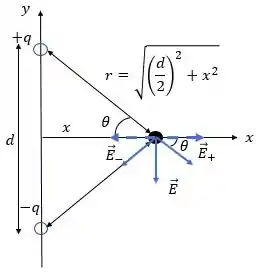
O que tá acontecendo aí: temos o dipolo e a origem do sistema no centro dele, ou seja, a carga positiva está acima do eixo e a carga negativa está abaixo, ok?
A distância do ponto que queremos calcular até a origem é . E a distância entre cada carga e o ponto é .
Temos que o campo elétrico gerado pela carga positiva estará na direção positiva de e o campo gerado pela carga negativa estará no sentido de , isso ocorre por conta dos sinais das cargas, show?
Dessa forma, podemos ver até pela figura, que as componentes no eixo dos campos se cancelam (estão em pontilhado ali), isso acontece por simetria: as duas cargas são iguais em módulo e estão a uma mesma distância do ponto.
Logo, sobrarão as duas componentes na direção negativa de . Como estamos interessados apenas no módulo do campo, não precisaremos da direção por enquanto, mas guarda para mais tarde rs. Assim, o campo resultante:
Como as duas cargas estão a uma mesma distância do ponto e possuem o mesmo valor em módulo: e:
Olhando para a figura, vemos que e que:
Com isso:
Onde , que é o campo para uma carga pontual. Dessa forma:
E:
Arrumando um pouquinho:
Simplificando o e sabendo que o momento dipolo :
E agora sim, vamos usar a informação de que esse campo elétrico estará na direção negativa de , logo .
Passo 2
(b) Vamos olhar com carinho para a fórmula do campo que achamos:
Se é muuuito grande, vai ser bem maior que também, ou seja, . E, com isso, . Logo, o se torna desprezível ali no denominador e o nosso campo se reduz a:
Arrumando esse denominador:
Prontinho, é isso que acontece quando é muito grande.
Resposta
(a), na direção .
(b)