Enunciado
Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 21.Exercício - Ex. 56
Uma carga de está uniformemente distribuída sobre a superfície da face de um disco não condutor de raio .
(a) Determine o módulo, a direção e o sentido do campo elétrico que esse disco produz em um ponto sobre o eixo do disco a uma distância de do seu centro.
(b) Suponha que a carga seja integralmente afastada do centro e uniformemente distribuída na periferia do disco. Ache o módulo, a direção e o sentido do campo elétrico no ponto .
(c) Se a carga for trazida integralmente para o centro do disco, aache o módulo, a direção e o sentido do campo elétrico no ponto .
(d) Por que o campo no item (a) é mais forte que o campo no item (b)? Por que o campo no item (c) é o mais forte de todos os campos?
Passo 1
(a) Vamos nos atentar ao seguinte: temos uma distribuição de carga negativa!! Dessa forma, o campo elétrico vai apontar sempre na direção do disco! Mas a ideia em si é a mesma de um disco com carga positiva, só vai mudar o sentido do campo elétrico. Vamos lá!
Bom, primeiro, vamos ver a fórmula para o campo elétrico de um disco sobre um ponto em seu eixo a uma distância :
A dedução dela aparece no exemplo 21.12 do livro! Onde , ou seja, é a densidade superficial de cargas do disco. Como a área de um disco é a área de um círculo:
E o nosso disco possui e uma carga :
E, substituindo esses valores na fórmula do campo elétrico, sabendo que e que o ponto está a de distância do centro do disco:
Fazendo as contas:
E esse campo elétrico vai apontar no eixo :
Já que seria algo desse tipo:
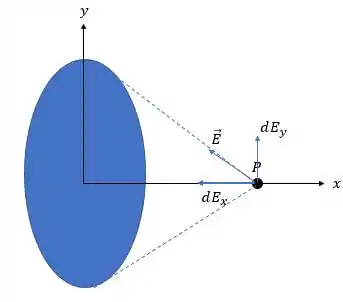
E aí, por argumento de simetria, a única componente que não será cancelada, será a componente . (Obs.: fica uma dica de como argumentar nessa situação, o argumento de simetria mata esse problema).
Passo 2
(b) Pensa aqui comigo: o disco é caracterizado por ter uma carga distribuída por toda a sua face, portanto, por toda a sua área, certo? Se essa carga for parar completamente na extremidade do disco, teremos um anel de cargas, né? Algo assim:
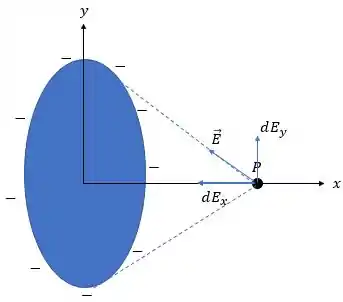
Se a gente desenhasse apenas onde tem carga:
Opa, isso é exatamente um anel carregado! Então, para achar o campo elétrico no ponto , vamos usar a fórmula para o campo de um anel carregado de raio sobre um ponto em seu eixo:
Onde já sabemos todos esses valores de , , e :
Fazendo as contas:
Pelos mesmos motivos do disco, esse campo elétrico também estará no eixo :
Passo 3
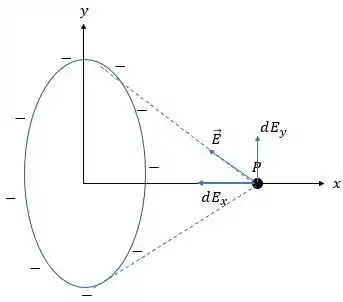
(c) Bom, se antes virou um anel carregado, o que você imagina que vai aparecer quando toda a carga for para o centro do disco? Vamos às imagens para te ajudar nessa:
Desenhando só onde tem carga:
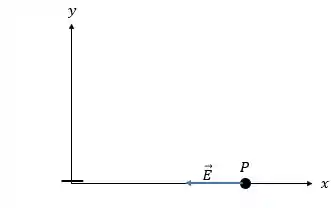
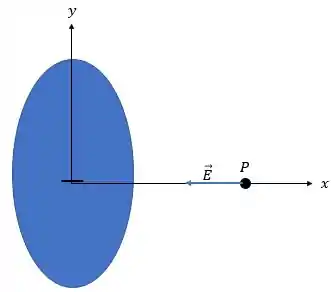
Ou seja, é basicamente uma carga pontual exercendo um campo elétrico em ! E qual a fórmula do campo elétrico de uma carga pontual?
Onde esse vai ser a distância ao ponto . Bom, já sabemos todos os valores:
E, como podemos ver na própria imagem, o campo estará no eixo :
Passo 4
(d) A resposta está nas distâncias das cargas ao ponto. Repare que em todas as fórmulas, o campo é inversamente proporcional à distância ao ponto de aplicação. Então, quanto mais distante, menor será o campo elétrico!
E olha para as distribuições de carga no disco:
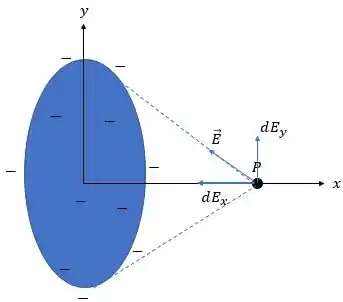
Existem cargas em todo o disco. Agora, olha o “anel”:
Existem cargas apenas na periferia do disco! Só que, quanto mais perto do centro do disco, mais perto a carga está de . Com isso, a gente vê, por comparação das imagens, que no “anel” as cargas estão majoritariamente mais distantes do que no disco. Logo, seu campo elétrico resultante será menor!
Da mesma forma, em (c), que tínhamos uma “carga pontual”:
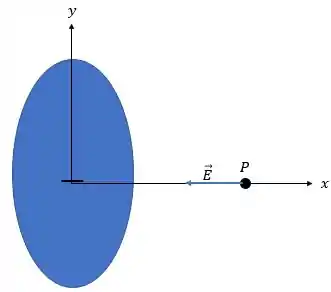
Toda a carga estava no centro do disco e, portante, no ponto mais perto de ! Com isso, seu campo elétrico acaba sendo o maior dos 3 casos. Beleza? 😉
Resposta
(a)
(b)
(c)
(d)Explicação no passo a passo.