Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Tipler - Vol 2- Ed: 6º - Capítulo 26.1 - Ex. 33

Considere que, na figura abaixo, o campo magnético tenha magnitude de 60   m T , a distância d seja de 40   c m e θ seja 24 ° . Determine a rapidez v com a qual a partícula entra na região e o ângulo ∅ de saída se a partícula é (a) um próton e (b) um dêuteron. Considero que m d = 2 m p

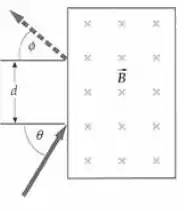
Passo 1

OPA, fala a boa, meu consagrado, para resolvermos essa questão precisaremos analisar a trajetória das partículas, pra isso, observe a figura abaixo.

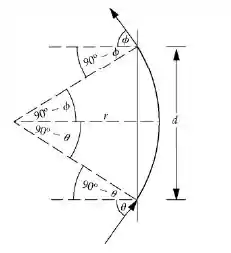
Agora que temos o diagrama para analizar, conseguimos estabelecer por simetria que ∅ =   θ , logo, ∅ = 24 ° ; Utilizando a trigonometria, temos que:

sin ⁡ 90 ° -   θ = s i n 66 °

d / 2 r = s i n 66 °

r = d 2   s i n 66 °

Agora utilizaremos a segunda Lei de Newton para determinar as velocidades v d e v p , SIGAM-ME OS BONS!!

Passo 2

Começaremos pelo próton:

F = m   a c

q p   v p   B = m p v p 2 r p

q p     B = m p v p r p

v p = q p   r p   B m p

Agora iremos substituir r:

v p = q p   d 2   s i n 66 °   B m p

v p = q p   d   B 2   m p s i n 66 °

v p = 1.602   x   10 - 19 C 0.40 m ( 60 m T ) 2   ( 1.673   x   10 - 27 k g ) s i n 66 °

v p = 1.3   x   10 6   m / s

MENOS UMA ALTERNATIVA! Agora vamos determinar a velocidade do dêuteron.

Passo 3

Será utilizada a mesma equação do Passo 2, só que agora com os valores estabelecidos para o dêuteron, então:

v d = q d   d   B 2   m d s i n 66 °

v d = q d   d   B 2   ( 2 m p ) s i n 66 °

v d = q d   d   B   4 m p s i n 66 °

v d = 1.602   x   10 - 19   C 0.40 m ( 60 m T )   4   ( 1.673   x   10 - 27 k g ) s i n 66 °

v d = 6.3   x   10 5   m / s

PRONTO, resolvemos tudo, nem foi difícil né, sussa demais, enfim, até a próximaaa.

Resposta

v p = 1.3   x   10 6   m / s

v d = 6.3   x   10 5   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um próton cuja trajetória faz um ângulo de 23º com a direção um campo magnético de 2,60 mT experimenta uma força magnética de 6,50 X 10- 17 N. Calcule (a) a velocidade do próton; (b) a energia cinétic
Determine a frequência de oscilação de um dipolo elétrico, de momento p e inércia rotacional I , para pequenas amplitudes de oscilaçāo em torno da sua posiçāo de equilíbrio em um campo elétrico E .
Determine o trabalho necessário para girar 180 ∘ um dipolo elétrico em um campo elétrico uniforme E → , em termos do momento de dipolo p e o ângulo inicial θ 0 entre p → e E → .
Um elétron é forçado a se mover ao longo do eixo do anel de cargas discutido na Seção 26-4. Mostre que o elétron pode desenvolver pequenas oscilações, através do centro do anel, com uma frequência dad