Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Tipler - Vol 2- Ed: 6º - Capítulo 25.1 - Ex. 49

Considere um fio de comprimento L na forma de um cone truncado. O raio do fio varia com a distância x até a extremidade estreira de acordo com r = a + b - a / L x , onde 0 < x < L . Deduza uma expressão para a resistência deste fio em termos de seu comprimento L , raio a , raio b e resistividade ρ .

Passo 1

Falaaa, meu povo.

A figura a seguir vai ilustrar as contas que vamos fazer.

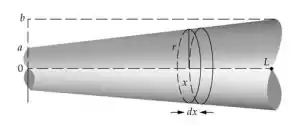
Considere um pequeno disco de raio r e comprimento d x . A resistência desse disquinho é

d R = ρ d x π r 2 = ρ d x π a + b - a L x 2

Notemos que esses discos estão todos em série, de forma que a resistência total será simplesmente a soma de cada uma das resistências d R . Em outras palavras,

R = ∫ d R R = ρ π ∫ 0 L d x a + b - a L x 2

Passo 2

Para calcular essa integral, fazemos a + b - a L x = u . Assim,

b - a L d x = d u ∴ d x = L b - a d u

Quando x = 0 , então u = a . Quando x = L , então u = b . Logo,

R = ρ π ∫ a b L b - a ⋅ 1 u 2 d u = ρ L π b - a 1 a - 1 b R = ρ L π a b

Resposta

A resistência é R = ρ L / π a b .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Dois fios de cobre cilíndricos têm a mesma massa. O fio A tem o dobro do comprimento do fio B. (Despreze quaisquer efeitos que a temperatura possa ter na resistência). Suas resistências estão relacion
Considere um fio metálico cujas extremidades estão conectadas aos terminais de uma bateria. Seu amigo diz que a rapidez de deriva dos portadores de carga no fio é a mesma, não importa o comprimento do
Os fios A e B são, ambos, feitos de cobre. Os fios estão conectados em série e, portanto, sabemos que eles conduzem a mesma corrente. Entretendo, o diâmetro do fio A é o dobro do diâmetro de B . Qual
Os fios A e B são feitos do mesmo material e têm o mesmo comprimento. O diâmetro do fio A é o dobro do diâmetro do fio B. Se a resistência de B é R, então qual é a resistência de A? (Despreze quaisque
Os diâmetros dos fios A e B são iguais. A corrente conduzida pelo fio A é o dobro da corrente conduzida pelo fio B. Em qual fio os portadores de carga têm a maior rapidez de deriva? (a) A, (b) B, (c)