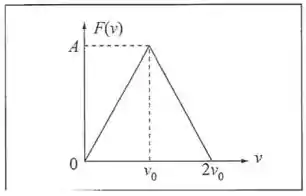
Considere um gás hipotético para o qual a função de distribuição de velocidades [definida na Seção 12.2(d)] tivesse a forma indicada na Fig. P.1. Calcule em função de : (a) A constante de normalização (fig.) (b) Os valores de , e para esta distribuição.

(b) Pra encontrar os valores de , e a gente vai ter que escrever uma função a partir do gráfico.

Vamos fazer um trecho de cada vez, começando com :

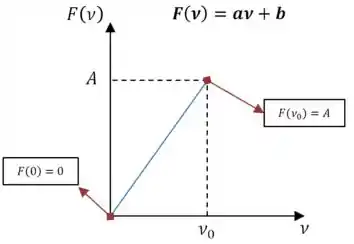
Com esses dois pontos a gente já consegue definir a equação:

Resolvendo o sistema o resultado vai ser o seguinte:

Então:

Agora vamos para o segundo trecho:

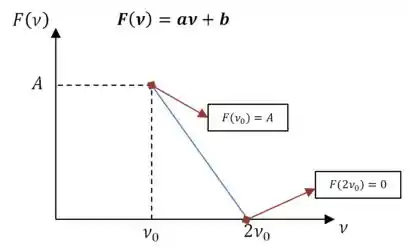
Substituindo a segunda equação na primeira:

E substituindo isso na segunda equação:

Pronto, agora já temos a função completa:

E a função é nula em qualquer outro ponto.

Agora a gente já pode começar a calcular os pontos que o enunciado pediu. Começando pelo .

Esse é o mais fácil, é simplesmente o “pico”. Ou seja, é a velocidade que dá o maior valor . Olhando o gráfico, dá pra ver que:

Ok, já o exige uma conta um pouco mais longa. A fórmula é essa aqui:

Substituindo com a função que a gente escreveu ali em cima:

Organizando um pouco:

Agora é só resolver as integrais:

Pra simplificar, vamos cortar em cada uma das frações:

Pronto! A velocidade média acabou sendo igual à velocidade de pico.

E agora, pra finalizar, temos que calcular a velocidade quadrática média.

É praticamente a mesma coisa do passo anterior, só que tem um a mais dentro da integral, e estamos integrando de a :

O primeiro passo é substituir a .

Agora é só resolver as integrais:

E simplificar:

Beleza, agora, pra calcular a velocidade quadrática média, é só lembrar do seguinte:

Pronto!