Enunciado
Física - Moysés - Vol. 2 - Ed: 4º - Capítulo 4.Problemas - Ex. 18
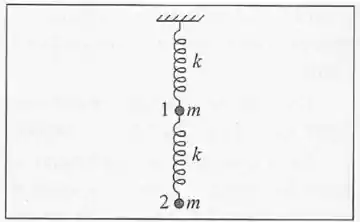
Uma partícula de massa está ligada por uma mola de constante elástica e massa desprezível a outra partícula de mesma massa, suspensa do teto por uma mola idêntica à anterior (figura). Inicialmente o sistema está em equilíbrio. Seja, e deslocamentos, a partir das respectivas posições de equil´brio, das partículas e , com o eixo dos orientado verticalmente para baixo. (a) Escreva as equações de movimento para e . (b) Obtenha os modos normais de oscilação vertical do sistema. Para isto, considere uma nova coordenada , combinação linear de e : . Escreva a equação de movimento para e procure determinar os coeficientes e de tal forma que esta equação para se reduza à equação de movimento de um oscilador harmônico simples. Você obterá duas soluções e , que se chamam as coordenadas normais (Seção 4.6). Calcule as frequências angulares de oscilação e associadas aos dois modos normais do sistema.
Passo 1
A distensão da mola de cima é exatamente igual à posição da massa . E a distensão da mola de baixo é .
Com isso fica fácil escrever as duas equações do movimento. Lembre que a lei de Hooke é:
Então para a primeira massa a gente pode escrever o seguinte:
E para a segunda massa:
Beleza, vamos organizar essas duas equações em um sistema:
E pra simplificar essas expressões, vamos definir uma constante nova:
Então:
Passo 2
(b) O próximo passo é procurar as coordenadas normais. Pra fazer isso nós vamos usar uma coordenada dessa forma:
A ideia é fazer com que essa coordenada obedeça a uma equação de oscilador harmônico:
Então vamos substituir a primeira equação nessa última:
E agora a gente vai usar aquelas equações no final do passo :
Os termos que multiplicam e dos dois lados têm que ser iguais:
Passo 3
E agora temos que resolver esse sistema pra encontrar e . Pela primeira equação:
E pela segunda:
Se a gente multiplicar as duas equações, o resultado vai ser o seguinte:
Dividindo os dois lados por :
E já podemos aproveitar pra encontrar as frequências que o enunciado pediu na letra (c). Simplificando um pouco essa última equação:
Isso é uma equação de segundo grau que a gente pode resolver pra encontrar :
E então a gente fica com duas soluções:
Beleza, agora continuamos resolvendo a letra (b).
Passo 4
A expressão que a gente tinha encontrado para e eram as seguintes:
Isso quer dizer que a nossa solução tem um grau de liberdade, ou seja, podemos escolher uma variável arbitrariamente sem prejudicar a solução.
Então vamos deixar e usar a segunda equação:
E agora vamos ter uma solução para cada :
E então a nossa coordenada normalizada fica assim:
Resposta
(a) As equações de movimento são .
(b) Os modos normais são e .
(c) As frequências angular são e .