Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 14.7 - Ex. 66
Considere o medidor venturi e a figura do Problema 65 sem o manômetro. Suponha que e que a pressão no ponto é . Calcule os valores (a) da velocidade V no ponto e (b) da velocidade no ponto para que a pressão no ponto seja zero. (c) Calcule a vazão correspondente se o diâmetro no ponto é . O fenômeno que ocorre em quando cai para perto de zero é conhecido como cavitação; a água evapora para formar pequenas bolhas.
Equação do Problema 65:
Figura do Problema 65:
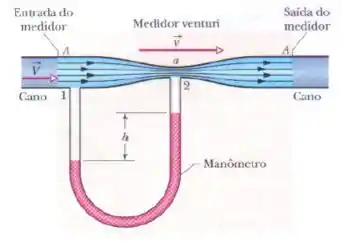
Passo 1
No próprio enunciado, recebemos a informação de que, naquele pedaço mais apertado do cano, a pressão cai para perto de zero, por isso podemos achar a diferença de pressão:
Beleza, agora é só substituir na fórmula, lembrando que a densidade da água é :
Cortando a área :
E essa é a reposta da letra (a).
Passo 2
A velocidade que acabamos de calcular surgiu quando supomos que a pressão no ponto era zero.
Então, pra achar o que a questão pede vamos simplesmente usar a equação da continuidade para descobrir qual é a velocidade associada à velocidade no tubo.
E essa é a resposta da letra (b).
Passo 3
A letra (c) quer saber qual é a vazão associada a essas velocidades se o diâmetro no ponto é .
Vamos começar calculando a área do cano quando o diâmetro é
Sabemos que a vazão é o produto da velocidade do fluido pela área do cano:
E essa é a resposta da letra (c).
Resposta
(a)
(b)
(c)