Exercícios de Equação de Bernoulli - Lista de Exercícios Resolvida
Questão 1
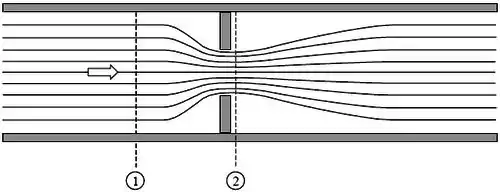
Observe o escoamento abaixo. Onde a velocidade deve ser maior, em (1) ou em (2)? Por quê?
Questão 2
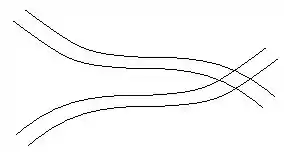
Podemos afirmar que, na figura abaixo, temos linhas de corrente? Por quê?
Questão 3
Considere as afirmativas:
- Linhas de corrente determinam a direção, módulo e sentido do vetor velocidade em um ponto de um escoamento
- Linhas de corrente determinam a direção e o sentido do vetor velocidade em um ponto de um escoamento
- Linhas de corrente determinam apenas a direção do vetor velocidade em um ponto de um escoamento
- Quanto mais afastadas estiverem as linhas de corrente, maior é a velocidade de um escoamento
- Linhas de corrente não se cruzam
Quais delas são verdadeiras?
Ver solução completaQuestão 4
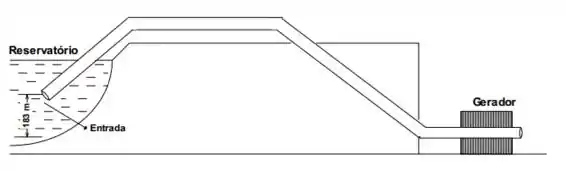
A área de entrada do tubo inferior do reservatório indicado na figura a seguir vale . A água entra neste tubo com uma velocidade de . No gerador, instalado a uma profundidade de abaixo do nível de entrada deste tubo, a área da seção reta é igual a e a água escoa com uma velocidade de nesta saída. Calcule a diferença de pressão em entre a entrada e a saída.
Questão 5
O abastecimento de água de um prédio é feito por uma tubulação, conforme o esquema a figura abaixo. Após passar por canos de seção reta e , a água segue por um cano de seção reta até sair( ponto 4) para a caixa d’água localizada no alto do edifício. Entre as posições 1 e 2 na tubulação é colocado um manômetro que mede a diferença de pressão . A altura do prédio é e o volume da caixa d’água é
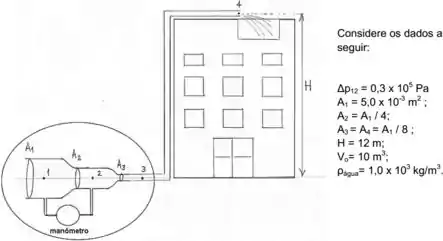
- Encontre a velocidade , no ponto 1 do encanamento.
- Determine a vazão no tubo e o tempo necessário pra encher a caixa d’água.
- Determine a velocidade , com que a água sai pela extremidade do tubo no alto do edifício.
- Determine a pressão manométrica no ponto 1(, que foi necessária para fornecer a vazão calculada.
Questão 6
Suponha que um vento com velocidade sopre sobre o telhado de uma casa, de seção reta com área . Qual o peso mínimo do telhado para evitar que este se solte? Suponha conhecida a densidade do ar.
Questão 7
Um riacho de efluentes industriais líquidos () de largura e profundidade corre a céu aberto.
O riacho passa a ser canalizado em uma tubulação com seção reta circular de diâmetro , que corre ao longo da horizontal de modo que o seu eixo central está a abaixo do nível médio do rio.
Finalmente, o líquido é lançado num jato horizontal para a atmosfera.
Observa-se que a velocidade do riacho, , é aproximadamente horizontal e uniforme ao longo de toda seção reta. Considere os fluxos sempre laminares e uniformes. Considere e .
Dado:
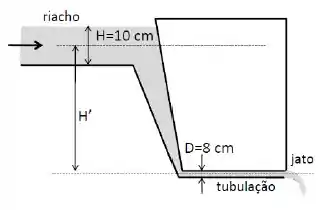
- Calcule a vazão do riacho.
- Calcule a velocidade do líquido dentro da tubulação horizontal.
- Calcule a pressão num ponto qualquer dentro da tubulação.
- Calcule a profundidade da tubulação.
Questão 8
Um fluido incompressível escoa suavemente pela tubulação mostrada na figura.
Assinale as relações corretas para as pressões e as velocidades do fluido nos pontos , , e indicados na figura:
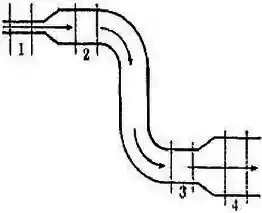
- e
- e
- e
- e
Questão 9
Água escoa suavemente pela tubulação cilíndrica da figura ao lado, preenchendo-a completamente. As secções 2 e 3 têm o mesmo diâmetro.
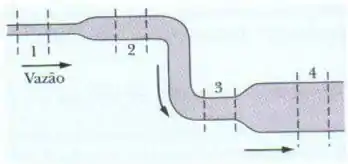
Na mesma tubulação, como se relacionam as pressões em cada região?
Questão 10
II. Um cano no porão de uma casa, com um diâmetro de , transporta água auma velocidade de e pressão de O cano se estreita para esobe para o segundo piso, acima do porão. Encontre a velocidade e a pressão da água no cano do segundo piso.
Ver solução completaQuestão 11
Um fluido incompressível escoa suavemente pela tubulação mostrada na figura.
Assinale as relações corretas para as pressões e as velocidades do fluido nos pontos , , e indicados na figura:
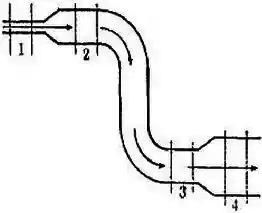
- e
- e
- e
- e
Questão 12
A figura abaixo mostra as linhas de corrente de escoamento em regime estacionário de um fluido incompressível através de uma tubulação cilíndrica de seção reta de área constante.
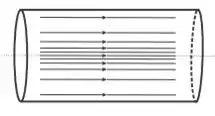
Baseado na figura, considere as seguintes afirmações:
- Uma vez que as linhas de corrente estão mais concentradas na região central do tubo, a pressão deve ser mínima próxima à superfície lateral da tubulação.
-As linhas de corrente na figura representam o escoamento estacionário de um fluido com viscosidade desprezível.
-A velocidade de escoamento do fluido é maior para as camadas mais próximas ao eixo do cilindro do que para as mais próximas à superfície lateral da tubulação.
São VERDADEIRAS as afirmativas:
- Somente
- Somente
- Somente
- Somente e
- Somente e
- Somente e
- Todas são verdadeiras
Questão 13
Um fluido incompressível de densidade escoa com velocidade por uma tubulação horizontal cilíndrica de raio inicial . A tubulação tem um estrangulamento, passando a ter raio , sendo . A tubulação é estreita o suficiente para que possamos desprezar diferenças de altura entre as linhas de corrente. Se a diferença de pressão entre os trechos 1 e 2 é ,qual o valor de ?
Questão 14
Um confeiteiro tem na sua gaveta duas seringas para inserir recheio de mel em um bolinho. Ambas têm o mesmo comprimento, mas uma delas tem diâmetro interno e a outra tem diâmetro . Podemos afirmar que:
- Se ele escolher a seringa de diâmetro , ele vai precisar fazer vezes mais pressão para obter a mesma vazão.
- Se ele escolher a seringa de diâmetro , ele vai precisar fazer vezes menos pressão para obter a mesma vazão.
- Se ele escolher a seringa de diâmetro , ele vai precisar fazer vezes mais pressão para obter a mesma vazão.
- Se ele escolher a seringa de diâmetro , ele vai precisar fazer vezes mais pressão para obter a mesma vazão.
- Não importa o diâmetro; a vazão em ambas será a mesma quando submetidas à mesma pressão.
Questão 15
Considere as seguintes afirmações:
- Quando um cano sofre redução em seu diâmetro, a velocidade e a pressão do fluido incompressível em seu interior aumenta, pois o fluido carrega mais momento linear.
- O jato d’água que vai de uma torneira fica mais estreito a medida em que avança.
- A expressão pode não ser constante ao longo de uma linha de corrente de um fluido compressível, pois depende da conservação das energias cinéticas e gravitacional.
São verdadeiras:
- Apenas a
- Apenas a
- Apenas a
- Apenas a e a
- Apenas a e a
- Apenas a e a
- Todas
- Nenhuma
Questão 16
Considere a equação de Bernoulli para fluxo incompressível:
Aplique a análise dimensional para cada um dos termos na equação e escreva qual é a dimensão de cada termo.
Ver solução completaQuestão 17
A figura abaixo mostra as linhas de corrente de um escoamento em regime estacionário de um fluido através da tubulação cilíndrica de seção reta de área constante.
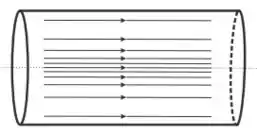
Baseado na figura, considere as seguintes afirmações:
- Uma vez que as linhas de corrente estão mais concentradas na região central do cilindro, a pressão deve ser mínima próxima a região lateral da tubulação.
-A equação de Bernoulli é válida entre quaisquer dois pontos da tubulação.
-A velocidade de escoamento do fluido é maior para as camadas do fluido mais próximas do eixo central do cilindro do que para as mais próximas à superfície lateral da tubulação.
São verdadeiras as afirmativas:
- Somente
- Somente
- Somente
- Somente
- Somente
- Todas são verdadeiras.
Questão 18
Um tanque cilíndrico pressurizado, com 5,0 m de diâmetro, contém água que emerge do tubo no ponto C, com uma velocidade de 38 m/s. O ponto A está localizado a 10 m acima do ponto B e o ponto C a 3 m acima do ponto B. A área do tubo no ponto B é de 0,09 e o tubo se estreita para uma área de 0,01 no ponto C. Suponha que a água é um fluido ideal com fluxo laminar. Na Figura ao lado, a pressão manométrica no ponto B, em kPa, é mais próxima:
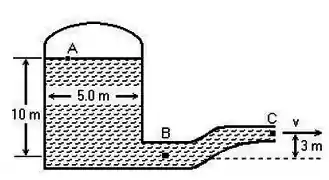
A) 740
B) 710
C) 770
D) 800
E) 820
Ver solução completaQuestão 19
Um fluido incompressível escoa de forma estacionária no interior de uma tubulação horizontal. Em um ponto da tubulação, a pressão é e o módulo da velocidade do fluido é . Em um outro ponto mais adiante na tubulação, a pressão é e o módulo da velocidade é . O que pode ser concluído em relação a e ?
(a)
(b)
(c)
(d)
(e)
(f) Apenas que .
(g) Apenas que .
Ver solução completaQuestão 20
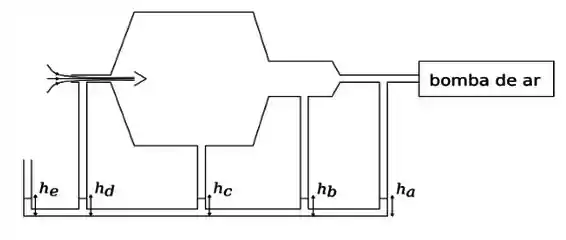
Qual a sequência correta entre as alturas ?
é a altura da coluna de líquido que repousa na parte de baixo do tubo.
Ver solução completaQuestão 21
Suponha que um vento com velocidade sopre sobre o telhado de uma casa, de seção reta com área . Qual o peso mínimo do telhado para evitar que este se solte? Suponha conhecida a densidade do ar.
Questão 22
Qual das seguintes afirmações é falsa quanto à derivação ou uso da equação de Bernoulli?
A) O fluido não deve ser viscoso.
B) Assumimos que o fluxo é estacionário.
C) O fluido deve ser incompressível.
D) O teorema trabalho-energia é usado para derivar a equação de Bernoulli.
E) As distâncias verticais são sempre medidas em relação ao ponto mais baixo do fluido.
Ver solução completaQuestão 23
Um fluido ideal de densidade , escoa através de um tubo horizontal com regiões 1 e 2, conforme ilustra a figura ao lado. Quando o fluido está na região 1, ele tem velocidade v1 = 0,20 m/s e pressão Pa. Sabendo que o diâmetro na região 2 é um quarto do diâmetro do tubo na região 1, responda às perguntas abaixo.
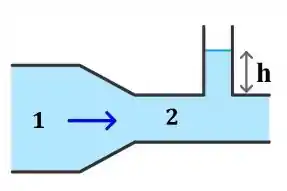
(a) Qual é a velocidade do fluido que atravessa a região 2?
(b) Qual é a pressão interna no cano da região 2?
(c) Se na região 2 há um tubo vertical com abertura para a atmosfera, qual é a altura h da coluna de fluido formada nessa abertura?
Ver solução completaQuestão 24
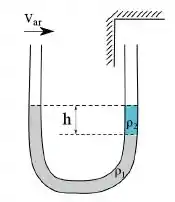
Determine em função da aceleração da gravidade , da densidade do ar no local e dos parâmetros indicados na figura.
Escolha uma:
Questão 25
Considere um sistema formado por um reservatório de água com área e altura . O reservatório está conectado na parte inferior com uma tubulação cuja seção transversal tem área . A uma distância da base do reservatório, a tubulação faz uma curva de 90 graus mantendo a seção transversal com a mesma área e ficando paralela ao solo. Em seguida, a tubulação se conecta com uma outra de área , cuja extremidade está aberta permitindo que a água saia com velocidade para o meio externo. Considere que a velocidade com que a superfície do líquido no reservatório desce seja muito menor do que as outras envolvidas no processo. Suponha conhecidas a densidade da água , a aceleração da gravidade e a pressão atmosférica .
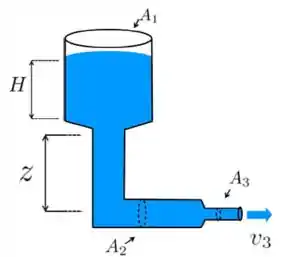
- Determine a velocidade no trecho horizontal de área em termos de
- Determine a pressão no trecho horizontal da canalização de área
Questão 26
II. Uma seringa contém um medicamento com a mesma densidade da água. A área de seção transversal do corpo da seringa é e a da agulha é .Na ausência de uma força no êmbolo, a pressão em qualquer lugar é de . Uma força de magnitude atua no êmbolo, fazendo com que o medicamentoesguiche horizontalmente da agulha.
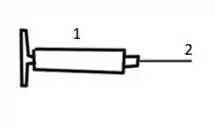
c) Determine a velocidade do medicamento ao sair da ponta da agulha.Bernoulli ().
d) Determine o tempo necessário para dispensar 1,0 cm3 do medicamento.
Dados:
Ver solução completaQuestão 27
Um avião requer uma diferença de pressão entre a superfície superior e inferior de sua asa
(sustentação) igual a . Suponha que o ar escoe de forma laminar (sem turbulência) sob a superfície inferior, com velocidade de . Considerando as faces da asa no mesmo nível e a densidade do ar sendo determine a velocidade do ar na superfíciesuperior da asa, para a sustentação desejada.
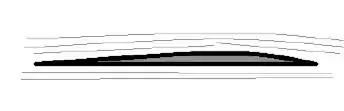
- 98,0m/s
Questão 28
Água flui da esquerda para a direita através do tubo horizontal mostrado na figura a seguir. No ponto , a área da seção reta vale e a velocidade da água é . No ponto a área vale . Nos tubos verticais que estão em contato com o horizontal a água está em repouso e em contato com a atmosfera nas suas extremidades superiores. A altura da coluna vertical de água no interior do tubo do lado direito é de enquanto a do lado esquerdo, , será determinada a seguir. Considere que a densidade da água vale Considere .
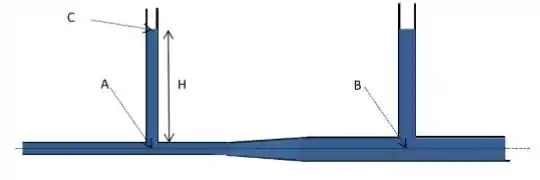
Qual a velocidade da água no ponto , em ?
A pressão no ponto se relaciona com a no ponto C de acordo com
Quanto vale, em , a altura ?
Ver solução completa
Questão 29
A água entra em uma casa através de um tubo com diâmetro interno de com uma pressão absoluta igual a . Um tubo com diâmetro interno de conduz ao banheiro do segundo andar, a de altura. Sabendo que no tubo de entrada a velocidade da água é igual a , qual a sua pressão na tubulação do banheiro? Considere a densidade da água como sendo e a aceleração da gravidade como sendo .
Ver solução completa
Questão 30
De uma barragem parte uma canalização de diâmetro interno , com poucos metros de extensão, havendo depois uma redução para . Do tubo de diâmetro , a água passa para a atmosfera sob a forma de um jato. A vazão foi medida, encontrando-se 100 L/s. Considerando o escoamento ideal, calcule:
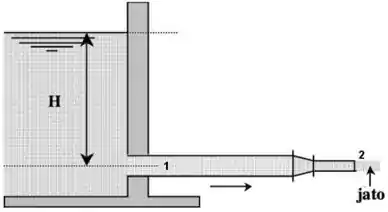
a) a pressão manométrica na parte inicial do tubo de diâmetro .
b) a altura H de água na barragem.
c) a densidade de energia cinética transportada pelo jato e a potência do jato (energia por unidade de tempo).
Ver solução completaQuestão 31
Um sistema de abastecimento de água consiste em um cano com diâmetro de entrada, de valor igual ao diâmetro de saída. A diferença de pressão entre as extremidades de entrada e de saída é igual a . Determine:
A diferença de altura entre as extremidades do cano .
Ver solução completaQuestão 32
Assinale a alternativa INCORRETA:
(a) De acordo com o Princípio de Pascal, uma variação de pressão aplicada a um fluido incompressível contido em um recipiente é transmitida integralmente a todas as partes do fluido e às paredes do recipiente;
(b) Dado que um objeto de madeira flutua em um fluido, a força de empuxo atuando sobre o objeto é maior que o peso do objeto. Isso ocorre porque a densidade do fluido é maior que a densidade do objeto em questão;
(c) Os fluidos são gases ou líquidos;
(d) A pressão _e uma medida da força por unidade de àrea exercida por um fluido;
(e) Um fluido ideal é incompressível, ou seja, sua massa específica tem um valor uniforme e constante;
(f) Se a velocidade de um fluido aumenta enquanto o fluido se move horizontalmente ao longo de uma linha de fluxo, a pressão do fluido aumenta.
Ver solução completaQuestão 33
Um fluido incompressível escoa suavemente (fluxo ideal) da esquerda para a direita pela tubulação da figura ao lado. Considerando como a vazão, como a velocidade e como a pressão do fluido, marque a resposta correta em relação às regiões 1 e 2 ilustradas na figura.
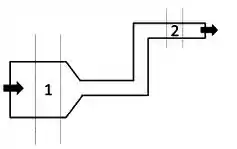
a) , ,
b) , ,
d) , ,
e) , ,
f) , ,
g) , ,
h) , ,
i) , ,
j) , ,
Ver solução completaQuestão 34
A água se move com uma velocidade 8,00 m/s em um cano com uma seção reta de a uma pressão de Pa. Em seguida, a água desce gradualmente metros enquanto a seção reta do cano aumenta para ao fim da descida. Determine a pressão da água logo após a descida. 
Questão 35
A área total das asas de um avião Airbus A380 é de aproximadamente . O peso dessa aeronave é de , parcialmente carregada. Numa decolagem, no referencial do avião, as velocidades do ar acima e abaixo das asas diferem. Seja a maior e a menor entre essas duas velocidades. Suponha que = 17,0. A densidade do ar sobre a pista é . Calcule, em , a velocidade mínima do escoamento acima das asas para que o A380 decole nas condições descritas acima. Despreze a ação de ventos.

Questão 36
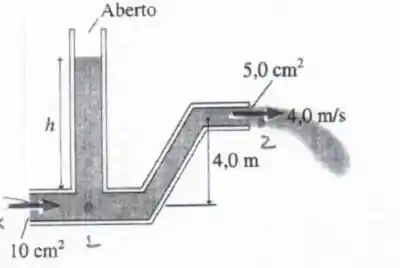
A figura mostra um esquema de captação de água para uma usina hidrelétrica. Mais à direita, um detalhe da saída do tubo no gerador quando a água já passou pela turbina. Sabendo que a diferença de pressão , que , , e determine (respostas com 3 algarismos significativos e em notação científica):
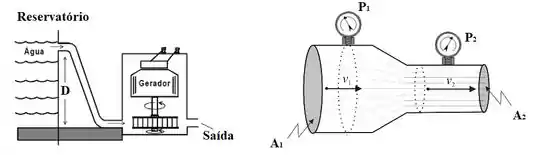
- A velocidade de escoamento
- Considere agora que a altura do espelho de água do reservatório em relação a entrada do tubo seja constante ao longo de um dia. Determine o volume total escoado pela usina em horas
- Determine a profundidade do tubo de entrada de água em relação a superfície de água no reservatório quando não há escoamento de água pela tubulação da turbina. Neste regime, a pressão na altura do tubo de entrada vale
Questão 37
Um tubo cilíndrico fechado de raio R e comprimento H é preenchido por um fluido de densidade ρ e colocado na vertical, conforme a figura ao lado. Um pequeno furo de raio na extremidade inferior do tubo é tampado por uma rolha. A pressão atmosférica é e a aceleração da gravidade é .
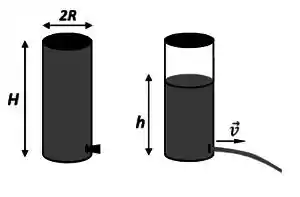
(a) Determine a força que o líquido exerce sobre a rolha.
(b) Determine a velocidade com a qual o fluido escoa pelo furo em função da altura h do líquido.
Determine a altura em que o fluido para de escoar.
Ver solução completaQuestão 38
A figura ao lado mostra uma grande represa de água doce que tem uma profundidade . Um cano horizontal de de diâmetro é inserido a uma profundidade , como ilustrado ao lado. Uma rolha fecha a abertura do cano.
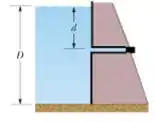
Determine o módulo da força de atrito entre a rolha e a parede do cano.
Quando a rolha é retirada, qual é o volume de água que sai do cano em 2 minutos? Use a equação de Bernoulli para obter esta resposta.
Ver solução completaQuestão 39
Em um grande reservatório de água, a entrada da tubulação (veja na figura) tem uma seção reta de e a velocidade da água é . A água desce gradualmente pelo tubo e na saída, a uma profundidade abaixo da entrada, a seção reta é vezes menor.
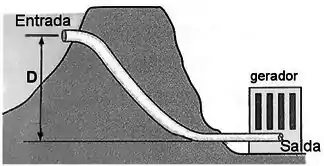
(a) Calcule a velocidade da água na saída.
(b) Calcule a diferença de pressão entre a entrada e a saída
Ver solução completaQuestão 40
A seção reta de um tubo horizontal sofre um alargamento. Se um fluido estiver escoando no sentido da seção mais estreita para a seção mais larga, o que acontecerá com: (I) a velocidade do fluido; (II) a pressão; (III) a vazão do fluido logo após a passagem pelo alargamento?
a) (I) diminui, (II) diminui, (III) aumenta
b) (I) aumenta, (II) aumenta, (III) diminui
c) (I) diminui, (II) diminui, (III) não muda
d) (I) aumenta, (II) não muda, (III) diminui
e) (I) aumenta, (II) diminui, (III) aumenta
f) (I) aumenta, (II) não muda, (III) aumenta
g) (I) diminui, (II) aumenta, (III) não muda
h) (I) não muda, (II) não muda, (III) não muda
Ver solução completaQuestão 41
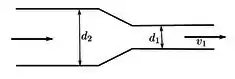
Um fluido incompressível com densidade escoa por uma tubulação horizontal e sai para o ar livre (a pressão atmosférica patm), com velocidade v1, após passar por um estrangulamento, no qual o diâmetro da tubulação diminui de d2 para d1. A pressão manométrica p2 - patm na tubulação, antes do estrangulamento, é dada por:
a)
b)
c)
d)
e)
f)
Ver solução completaQuestão 42
Uma caixa d'água hemisférica com raio R = 2 m está completamente cheia de água e com seu ponto mais baixo suspenso a uma altura H = 23 m do solo. O topo da caixa d'água está fechado com um teto plano na horizontal (ver figura). O fundo da caixa está conectado a um cano com 10 cm de raio e que se estende até o solo. Se a água no cano escoa em regime estacionário e com velocidade v2 = 20 m/s, determine:
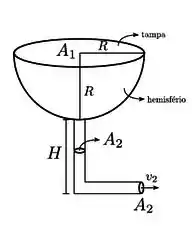
(a) (1,0) A velocidade de escoamento da água no topo da caixa d’água.
(b) (2,0) Determine a pressão no topo da caixa d'água, entre a tampa e a superfície da água. Neste item considere que a velocidade no topo da caixa d'água é muito menor que a velocidade no cano v2.
Dados: Pressão atmosférica patm = Pa, densidade da água ρ = 103 kg/m3 e a aceleração gravitacional g = 10 m/s2.
Ver solução completaQuestão 43
A figura mostra quatro tubos nos quais a água escoa suavemente para a direita. Os raios das diferentes partes dos tubos estão indicados. Em qual dos tubos o trabalho total realizado sobre um volume unitário de água que escoa da extremidade esquerda para a extremidade direita é nulo?
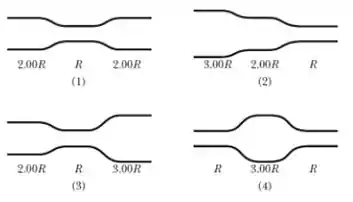
a)1 e 4;
b) apenas 2;
c) 1 e 3;
d) apenas 4;
e) apenas 3;
Ver solução completaQuestão 44
A figura abaixo mostra um esquema de um tubo de Pitot, que é usado para medir a velocidade do ar nos aviões. Ele é formado por um tubo externo com pequenos furos B (quatro são mostrados na figura) que permitem a entrada de ar no tubo; este tubo está ligado a um dos lados de um tubo em de U. O outro lado do tubo em forma de U está ligado ao furo A na frente do medidor, que aponta no sentido do movimento do avião. Em A o ar fica estagnado, de modo que . Em B, porém, a velocidade do ar é presumivelmente igual à velocidade do ar em relação ao avião. Considere a diferença de altura entre A e B desprezível.
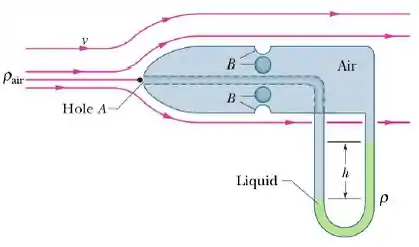
a) Seja ρ a massa específica do líquido contido no tubo em U e h a diferença entre os níveis do líquido no tubo.Sendo a densidade do ar , encontre a expressão que determina a velocidade do avião.
b) Suponha que o tubo contém um liquido cuja massa específica é e que a diferença de nível medida é 40,0 cm. Qual é a velocidade do avião em relação ao ar? A massa específica do ar é .
Ver solução completaQuestão 45
A água é bombeada através da mangueira mostrada abaixo, de um nível mais baixo para um nível mais alto . Comparada com a água no ponto , a água no ponto :
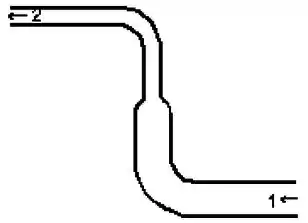
(a) tem maior velocidade e menor pressão
(b) tem maior velocidade e maior pressão
(c) tem menor velocidade e menor pressão
(d) tem menor velocidade e maior pressão
(e) tem maior velocidade e a mesma pressão
Ver solução completaQuestão 46
Numa seção de tubo horizontal com um diâmetro de a pressão é de e água flui a uma velocidade de . O tubo se estreita para . Qual é a pressão na região mais estreita se a água se comportar como um fluido ideal de densidade de ?
Atenção: esboce na figura abaixo as linhas de fluxo e se utilizar Bernoulli indique os pontos em que a equação foi aplicada.
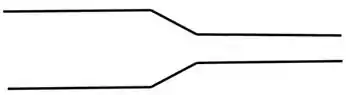
A) 4,00 kPa
B) 7,50 kPa
C) 5,82 kPa
D) 6,42 kPa
E) 4,61 kPa
Ver solução completaQuestão 47
Um líquido escoa da esquerda para a direita no cano mostrado na figura. Os pontos A e B estão na mesma altura, mas a área da seção reta do cano é diferente nos dois pontos. Os pontos B e C estão em alturas diferentes, mas a área da seção reta do cano é igual nos dois pontos. Indique a relação correta entre as pressões nos três pontos.

a) PB > PA e PB >PC;
b) PA > PB > PC;
c) PC > PB > PA;
d) PB > PA > PC;
e) PC > PA e PC >PB;
Ver solução completaQuestão 48
Um cano de água entra em uma casa 2,0 m abaixo do nível do solo. Um cano de menor diâmetro leva água a uma torneira situada no segundo andar, 5,0 acima do solo. A velocidade da água é 2,0 m/s no cano principal e 7,0 m/s no segundo andar. Tome a massa específica da água como sendo Se a diferença de pressão no cano principal Pa, a pressão no segundo andar é:
- , com o cano principal na pressão mais alta.
- , com o cano principal na pressão mais baixa.
- , com o cano principal na pressão mais alta.
- , com o cano principal na pressão mais alta.
- , com o cano principal na pressão mais baixa.
Questão 49
Água flui no tubo horizontal mostrado na figura abaixo. No ponto A, a área é de e a velocidade da água é de . Em B, a área é de . O fluido no tubo superior é mercúrio, que tem uma densidade de . Podemos tratar a água como um fluido ideal com uma densidade de .
Qual é a altura ?
ATENÇÃO: ESBOCE NA FIGURA ABAIXO AS LINHAS DE FLUXO E SE UTILIZAR BERNOULLI
INDIQUE OS PONTOS EM QUE A EQUAÇÃO FOI APLICADA.
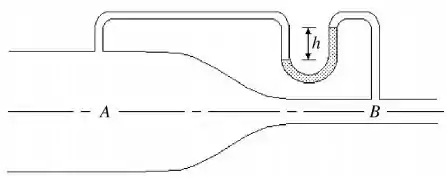
A) B) C) D) E)
Ver solução completaQuestão 50
De modo a medir a vazão de saída de uma tubulação de água, foi instalado um manômetro (medidor de pressão que mede a diferença entre a pressão real e a pressão atmosférica). Ao final da tubulação, colocou-se uma restrição, cuja área de seção reta é igual a da área de seção reta da tubulação principal. O manômetro, colocado na posição mostrada na figura, indica pressão igual a . Determine o valor da velocidade de escoamento na saída da tubulação:
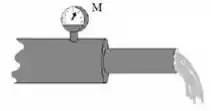
A) Faltam dados para determinar
B)
C)
D)
E)
Ver solução completaQuestão 51
A figura ao lado ilustra um recipiente cilíndrico (cilindro reto, de base circular) de área transversal , contendo líquido ideal de densidade . O cilindro é aberto para a atmosfera (pressão atmosférica ) na sua parte superior. A uma distância abaixo da superfície do líquido existe uma torneira cilíndrica de área transversal , por onde o fluido pode escoar com velocidade . Por outro lado, a velocidade da superfície do fluido é denotava por . Considere que a aceleração da gravidade no local é constante e representada por , como indicado na figura.
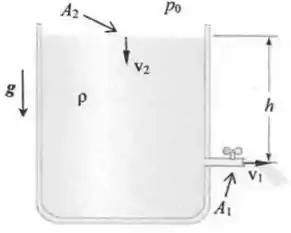
- Usando a equação da continuidade, escreva em termos de , e .
- Usando a equação de Bernoulli, calcule o valor de . Expresse seu resultado em termos de , , e .
- Suponha que a tampa seja colocada na parte superior do cilindro e que o ar entre a tampa e o líquido seja mantido a pressão constante. Para esta situação, calcule o ovo valor de . Na sua resposta deste item considere que , de tal forma que . Expresse seu resultado em termos de , , , e .
Questão 52
Uma grande caixa d’água, aberta na parte de cima, tem um pequeno furo no fundo. Quando o nível da água está a 20 m acima do fundo da caixa, a velocidade da água que sai pelo furo é:
a) 2,5 m/s;
b) 20 m/s;
c) 40 m/s;
d) não pode ser calculada, a menos que seja fornecida a área do buraco;
e) não pode ser calculada, a menos que sejam fornecidas as áreas do buraco e do tanque;
Ver solução completaQuestão 53
Considere um tanque onde a água pode escoar para fora passando por dois canos com seção retas de áreas diferentes. No exterior do tanque temos a pressão atmosférica . A área do cano exterior é e a do cano interior é . A altura é desconhecida, e a área do tanque é muito maior que a área dos canos. A vazão através do cano é de .
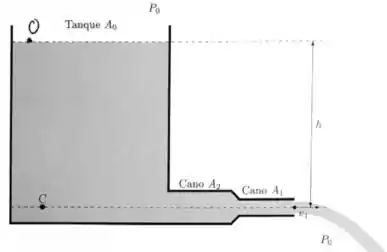
(a) Calcule a velocidade de saída da água.
(b) a velocidade da água ao longo do cano de área .
(c) a altura .
(d) a pressão manométrica dentro do cano de área .
(e) a pressão manométrica no ponto supondo que ele se encontra tão distante dos canos que a velocidade do fluido pode ser considerada nula.
Ver solução completaQuestão 54
O abastecimento de água de um prédio é feito por uma tubulação, conforme o esquema a figura abaixo. Após passar por canos de seção reta e , a água segue por um cano de seção reta até sair( ponto 4) para a caixa d’água localizada no alto do edifício. Entre as posições 1 e 2 na tubulação é colocado um manômetro que mede a diferença de pressão . A altura do prédio é e o volume da caixa d’água é
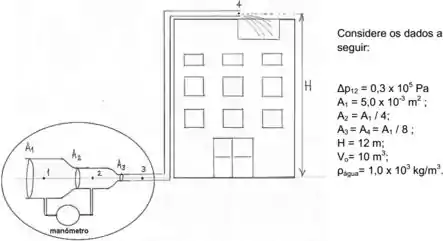
- Encontre a velocidade , no ponto 1 do encanamento.
- Determine a vazão no tubo e o tempo necessário pra encher a caixa d’água.
- Determine a velocidade , com que a água sai pela extremidade do tubo no alto do edifício.
- Determine a pressão manométrica no ponto 1(, que foi necessária para fornecer a vazão calculada.
Questão 55
Um riacho de efluentes industriais líquidos () de largura e profundidade corre a céu aberto.
O riacho passa depois a ser canalizado em uma tubulação com seção reta circular de diâmetro , que correão longo da horizontal de modo que o seu eixo central está a abaixo do nível médio do rio.
Finalmente, o líquido é lançado num jato horizontal para a atmosfera.
Observa-se que a velocidade do riacho, , é aproximadamente horizontal e uniforme ao longo de toda seção reta. Considere os fluxos sempre laminares e uniformes. Considere e .
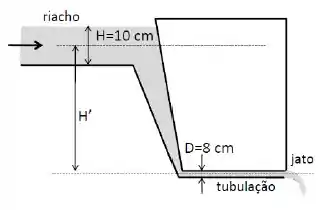
- Calcule a vazão do riacho.
- Calcule a velocidade do líquido dentro da tubulação horizontal.
- Calcule a pressão num ponto qualquer dentro da tubulação.
- Calcule a profundidade da tubulação.
Questão 56
Na mangueira da figura abaixo, a água passa de um nível mais baixo para um nível mais alto. Comparada com a água no ponto , a água no ponto :
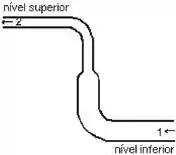
- tem maior velocidade e menor pressão.
- tem maior velocidade e maior pressão.
- tem menor velocidade e menor pressão.
- tem menor velocidade e maior pressão.
- tem maior velocidade e a mesma pressão.
Questão 57
Um recipiente vedado, com a forma indicada na figura 1 é totalmente preenchido por um fluido ideal. As pressões em dois pontos do fluido neste recipiente são indicadas por (no ponto ) e (no ponto ). A figura 2 mostra um tubo que sofre estreitamento e pelo qual escoa (escoamento estacionário) um fluido ideal incompressível. As pressões em dois pontos do fluido neste tubo são indicadas por (no ponto) e (no ponto ). É correto afirmar:
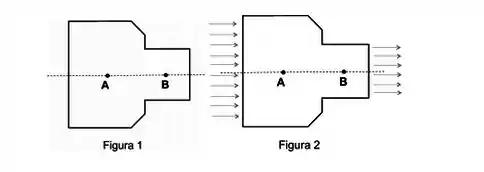 .
.
- .
Questão 58
Considere um escoamento estacionário de um fluido numa canalização horizontal com área de seção reta constante, uma linha de corrente, também horizontal, e dois pontos distintos nesta linha, 1 e 2. Se a velocidade do fluido for a mesma nos dois pontos, marque a alternativa que relaciona corretamente a densidade e a pressão do fluido no ponto 1, e , à densidade e à pressão do fluido no ponto 2, e :
(a) > , > .
(b) > , = .
(c)
(d) = , = .
(e) = ,
(f) = , > .
Ver solução completaQuestão 59
Um fluido incompressível de viscosidade desprezível é bombeado continuamente para a extremidade mais estreita de um cano longo, cuja largura aumenta continuamente, e sai do cano na outra extremidade. A pressão na entrada é maior que a pressão na saída. Uma possível explicação é que:
- a velocidade do fluido aumenta da entrada para a saída.
- a saída está em um ponto mais alto que a entrada.
- a saída está em um ponto mais baixo que a entrada.
- a velocidade do fluido é a mesma nas duas extremidades.
- a saída está na mesma altura que a entrada.
Questão 60
Há um recipiente cuja altura e área são dadas por e , respectivamente. Ele é conectado com um tubo cuja área é como mostrado na figura abaixo. O recipiente é cheio com um fluido de densidade de massa . A área do recipiente é suficientemente grande para podermos ignorar a velocidade da superfície do fluido (ponto A). Por outro lado, a pressão na saída do tubo (ponto B) é dada pela pressão atmosférica . Podemos ignorar o raio do tubo comparado com e . Considere a constante gravitacional conhecida.
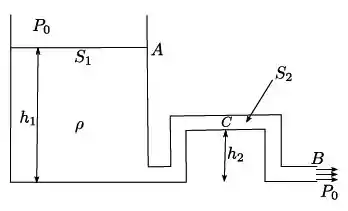
- Considerando que a saída do tubo fica na mesma altura que o fundo do recipiente, calcule a velocidade do fluido no ponto B.
- Calcule a pressão no ponto C, que fica a uma altura do fundo do recipiente.
Questão 61
Um tanque aberto na parte superior contém uma grande quantidade de água (de densidade ) que pode ser esgotada por meio de um cano ligado à sua parte inferior. A secção reta do cano na região do ponto , localizado a uma altura abaixo do nível da água, é , e na região , localizado a uma altura abaixo de , é . No final do encanamento existe uma válvula . Considere que a área da superfície do tanque é muito maior que área da secção reta da tubulação. Calcule:
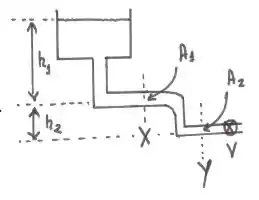
- A pressão nos pontos e com a válvula fechada.
- A velocidade da água no ponto com a válvula aberta.
- A pressão no ponto com a válvula aberta.
Questão 62
Um grande tanque é cheio com água até 15m de altura. Um bico localizado a 10,0 m acima do fundo do tanque é então aberto, como mostrado na figura abaixo. Com que velocidade a água deixa o bico?
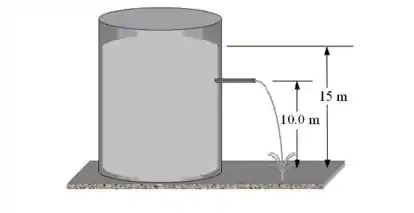
Use:
Ver solução completaQuestão 63
(Cap 14 - Ex 44) Uma bebida leve (essencialmente água) escoa em um tubo de uma fábrica de cerveja com uma vazão volumétrica tal que deve encher 220 latas de 0,355 L por minuto. Em um ponto do tubo, a pressão manométrica é igual a 152kPa, e a área da seção reta é igual a 8,0 . Em um ponto 1, situado 1,35m acima do ponto 2, a área da seção reta é igual a 2,0 . Obtenha a) a vazão mássica; b) a vazão volumétrica; c) as velocidades do escoamento nos pontos 1 e 2; d) a pressão manométrica no ponto 1.
Ver solução completaQuestão 64
(Cap 14 - Ex 43) As linhas de correntes horizontais em torno das asas de um pequeno avião são tais que a velocidade sobre a superfície superior é igual a 70,0m/s e sobre a superfície inferior é igual a 60,0m/s. Se a área da asa é igual a 16,2 , qual é a força vertical resultante (incluindo o efeito da gravidade) sobre o avião? A densidade do ar é igual a .
Ver solução completaQuestão 65
Um sistema horizontal de tubos, que proporciona um fluxo constante de água, é construído a partir de tubos com diferentes diâmetros, como mostrado na figura abaixo. Em qual dos pontos marcados a água no tubo apresenta maior pressão? O desenho é uma vista de cima do tubo.
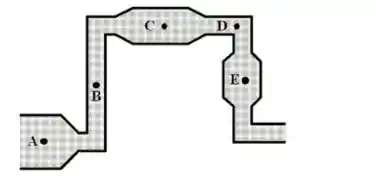
- A
- B
- C
- D
- E
Questão 66
O esquema ao lado mostra a vista lateral de uma tubulação na qual água flui idealmente no sentido indicado. No ponto , a velocidade é e a pressão é . A área da seção transversal da tubulação nos pontos e é um terço da área da seção transversal em e . Considere e .
Calcule a velocidade do fluido nos pontos e .
Calcule a pressão nos pontos e . Em qual desses pontos a pressão é menor? Explique sua resposta.
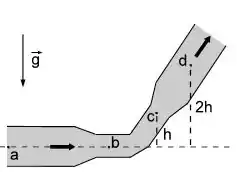
Questão 67
O diâmetro de um tubo horizontal sofre aumento para o dobro de seu valor inicial. Se um fluido ideal estiver escoando de forma estacionária da seção estreita para a larga, então:
(a) A velocidade e a pressão diminuirão.
(b) A velocidade diminuirá mas a pressão aumentará.
(c) A velocidade aumentará mas a pressão diminuirá.
(d) A velocidade e a pressão aumentarão.
(e) A velocidade OU a pressão se modificará, mas NÃO ambas.
Ver solução completaQuestão 68
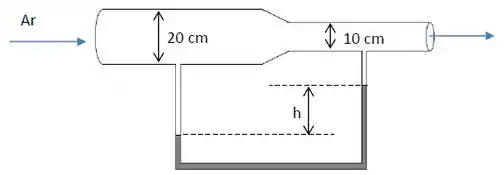
O ar escoa através de um tubo de vazão de . O tubo consiste em duas seções com diâmetros de e com uma seção de redução suave que as conecta. A diferença de pressão entre as duas seções do tubo é medida por u manômetro de água. Desprezando os efeitos de atrito e considerando a densidade do ar , determine:
(a) a velocidade do ar ao passar pelo tubo de maior diâmetro
(b) a razão entre as velocidades do tubo maior e o tubo menor
(c) a altura entre as duas superfícies da água nas seções do tubo.
Questão 69
O suprimento de água de uma casa é feito por um tubo de 4 cm de diâmetro (ponto 1). Um tubo com diâmetro de 2 cm leva a água a uma altura de 7 m até a caixa d’água (ponto 2). A bomba coloca 600 L de água na caixa em 10 minutos. Considere o escoamento ideal.
a) Calcule a velocidade com que a água sai para a caixa.
b) Calcule a pressão manométrica que a bomba deve manter no ponto 1.
c) Calcule a potência da bomba para manter essa vazão.
Ver solução completaQuestão 70
A água é bombeada através da mangueira mostrada abaixo, de um nível mais baixo (1) para um nível mais alto (2). Comparada com a água no ponto 1, a água no ponto 2:
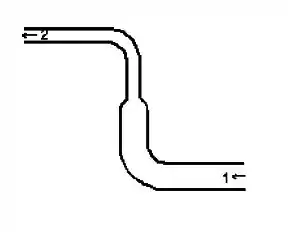
a) tem maior velocidade e menor pressão;
b) tem maior velocidade e maior pressão;
c) tem menor velocidade e menor pressão;
d) tem menor velocidade e maior pressão;
e) tem maior velocidade e a mesma pressão;
Ver solução completaQuestão 71
A figura mostra um sifão, que é um tubo usado para transferir líquidos de um recipiente para outro. O tubo ABC deve estar inicialmente cheio e nesta condição o líquido escoa pelo tubo até que a superfície do líquido no recipiente esteja no mesmo nível que a extremidade A do tubo. O líquido tem uma massa específica de 1000 kg/m³ e viscosidade desprezível. As distâncias mostradas na figura são h1= 25 cm e h2= 45 cm. Considere a área da seção reta do sifão constante.
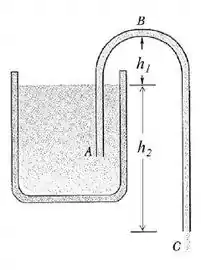
(a) Com que velocidade o líquido sai do tubo no ponto C?
b) Se a pressão atmosférica é , qual é a pressão do líquido em B, o ponto mais alto do tubo?
Ver solução completaQuestão 72
(Cap 14 - Ex 39) Um tanque selado que contém água do mar até uma altura igual a 11,0m também contem ar acima da água a uma pressão manométrica igual a 3,0atm. A água escoa para fora através de um pequeno orifício na base do tanque. Calcule a velocidade de efluxo da água.
Ver solução completaQuestão 73
A água sai de uma torneira aberta de forma a formar um feixe que se afina, sem se dividir, conforme a água flui em direção ao ralo, como indica a figura. Supondo que a seção transversal deste feixe se mantém circular no decorrer do fluxo, com raio e velocidade da água imediatamente após sair da torneira, e considerando a água um fluido incompressível sem viscosidade (considere a aceleração da gravidade conhecida), estime:
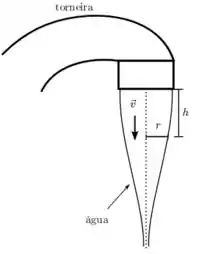
- A velocidade do fluido , em função da diferença de altura a partir da torneira.
- O raio de seção transversal do feixe, em função do módulo de velocidade nesta seção do fluido.
- O raio de uma seção transversal de um feixe, , agora em função da diferença de altura a partir da torneira.
Questão 74
Um reservatório contém água até de altura e sobre a água, uma camada de óleo de densidade , também com de altura. Abre-se um pequeno orifício na base do reservatório. Qual é a velocidade de escoamento da água?
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 75
Gás flui no tubo abaixo. Você não consegue ver os diâmetros nos pontos e . Qual a sequência correta entre as velocidades .
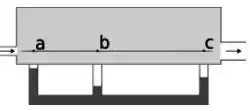
Ver solução completa
Questão 76
Água flui da esquerda para a direita através do tubo horizontal mostrado na Figura a seguir. No ponto A , a área da seção reta vale 4,00 cm2 e a velocidade da água é VA =6,00 m/s. No ponto B a área vale 10,0 cm2 . Nos tubos verticais que estão em contato com o horizontal a água está em repouso e em contato com a atmosfera nas suas extremidades superiores. A altura da coluna vertical de água no interior do tubo do lado direito é de 200 cm enquanto a do lado esquerdo, H , será determinada a seguir. Seja ρ a a densidade da água. Considere g=10,0 m/s 2 . Responda as questões 5 e 6.
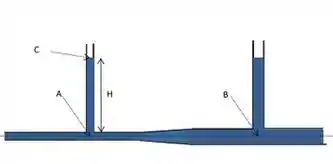
Quanto vale, em cm, a altura H?
A) 31
B) 49
C) 80
D) 231
E) 249
Ver solução completaQuestão 77
A figura mostra o desenho de um túnel cavado por um cachorro da savana. A geometria e o posicionamento da entrada e da saída do túnel, correspondentes a dois buracos, asseguram que o vento que sopra sobre o buraco número 2 sempre terá uma velocidade mais baixa do que aquele que sopra sobre o buraco número 1. Podemos afirmar que:
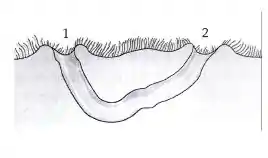
- O ar flui através do túnel, do buraco 2 para o buraco 1, ventilando o ambiente.
- O ar flui através do túnel, do buraco 1 para o buraco 2, ventilando o ambiente.
- O ar dentro do túnel não é afetado. Os dois buracos servem apenas para rota de fuga do animal.
- Nada se pode afirmar com as informações disponíveis.
Questão 78
Um reservatório cilíndrico circular de diâmetro contém um combustível líquido com densidade , suposto ideal, Esse reservatório possui uma tampa pesada, de massa , que pode se mover verticalmente, em m contato permanente com o fluido e exercendo pressão sobre sua superfície. Acima da tampa existe ar à pressão atmosférica. Na região lateral desse reservatório, mais abaixo, há uma abertura com uma válvula conectada a um tubo horizontal de diâmetro , para escoar o fluido. A válvula é aberta quando a distância vertical entre a superfície do líquido e o centro do tubo é de . Considere .
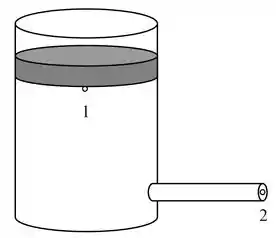
Calcule a velocidade do fluido no tubo horizontal.
Determine a vazão e a velocidade de descida da tampa.
Coloca-se, na extremidade do tudo, um bico com diâmetro de saída igual à metade do diâmetro do tubo. Determine a nova vazão e a pressão manométrica no centro do tubo.
Ver solução completaQuestão 79
Na figura abaixo, a água escoa suavemente pela tubulação descendo uma altura do ponto 1 ao ponto 4. Os pontos 1 e 2 estão na mesma altura, assim como os pontos 3 e 4. A área da seção reta no ponto 1 é . As áreas das seções retas dos tubo em 4,3 e 2 têm a relação:
Mede-se a diferença de pressão entre os pontos 4 e 1 e obtém-se . Considere ,
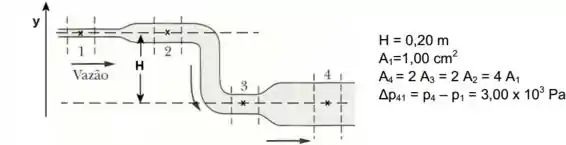
- Determine a expressão para a velocidade de escoamento no ponto 1, , em função de , , e . Calcule essa velocidade
- Determine a diferença de pressão entre os pontos 3 e 4, .
- Calcule a velocidade do nível da água na caixa quando as vazões nos apartamentos são e respectivamente. ( Dê a resposta em e ).
A figura representa uma caixa d’água alimentada com água bombeada à razão de litros por minuto. A superfície livre de água na caixa tem área . Dois canos( 1 e 2) distribuem a água a dois apartamentos.
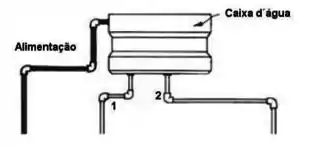
Questão 80
Um fluido incompressível flui da esquerda para a direita por uma tubulação de seção reta circular com diâmetro variável. A figura mostra apenas um pedaço da tubulação, que sai para a atmosfera no ponto . A densidade do fluido é de e os diâmetros das seções transversais em e em são iguais a e , respectivamente. O ponto está acima do ponto . Deseja-se uma vazão de saída de .
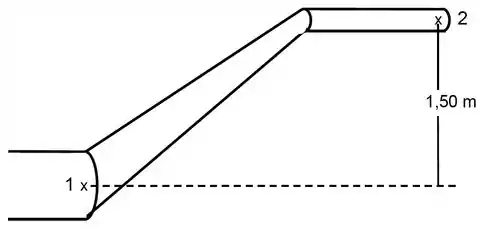
Determine quais devem ser as velocidades de escoamento no ponto , , e no ponto ,
Determine a pressão manométrica a que deve estar submetido o fluido no ponto para que se obtenha a vazão desejada.
Calcule a potência necessária para fornecer essa vazão.
Ver solução completaQuestão 81
Um cano contém um fluido em repouso. Para aplicar a equação de Bernoulli a essa equação,
- fazemos , pois não há movimento.
- fazemos .
- fazemos iguais a zero.
- fazemos , pois não há aceleração.
- isso é impossível, pois a equação de Bernoulli se aplica apenas a fluidos em movimento.
Questão 82
Um fluido passa por um tubo cuja seção reta varia conforme a figura abaixo. Em qual das seções ilustradas a pressão do fluido é mínima?
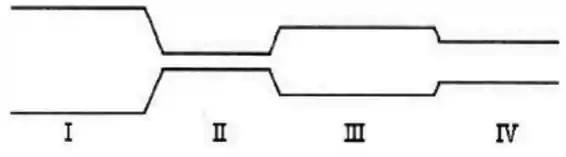
A pressão é sempre a mesma ao longo do tubo.
Ver solução completaQuestão 83
(Cap 14 - Ex 46) Um sistema de irrigação de um campo de golfe descarrega a água de um cano horizontal à taxa de . Em um ponto do cano em que o raio é 4,0cm, a pressão absoluta da água é . Em um segundo ponto do cano, a água passa por uma constrição, onde o raio é 2,0 cm. Qual é a pressão absoluta da água ao passar por essa constrição?
Ver solução completaQuestão 84
Um reservatório A com superfície fechada, é conectado a um tubo B, aberto para a atmosfera, com área de seção reta constante e muito menor que a superfície de água em A, como mostra a figura.
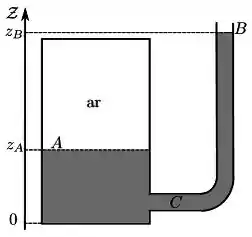
Considerando que existe um fluxo de água entre esses dois reservatórios, a velocidade da água no ponto C, indicado na figura, é dada por:
Questão 85
Na tubulação da figura ao lado, um fluxo estacionário de água passa de um nível mais baixo para um nível mais alto partindo da região 1 de diâmetro , passado pela região 2 de diâmetro e chegando à região 3 de diâmetro . Onde, . Sendo a pressão na região 1 e a velocidade do fluido na região 1, e assim por diante, marque a alternativa correta.
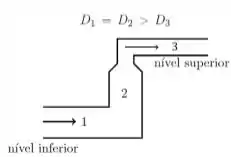
Ver solução completa
Questão 86
A figura abaixo mostra uma caixa d’água numa certa altura ligada a uma tubulação que desce e depois sobe, tendo sua seção reta reduzida no ponto mais baixo. O nível da água na caixa (ponto ) está a uma altura . A altura da extremidade do tubo (ponto ) está a uma altura . Os pontos e estão a mesma altura . Considere as seguintes situações:
(I) – A extremidade está vedada com uma tampa
(II) – A extremidade está totalmente aberta para a atmosfera.
Comparando a pressão no ponto com a pressão no ponto em cada caso, podemos afirmar que:
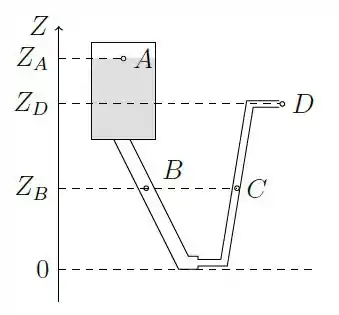
(a) Tanto na situação I como na situação II,
(b) Tanto na situação I como na situação II,
(c) Na situação I, , na situação II,
(d) Na situação I, , na situação II,
(e) Na situação I, , na situação II,
Ver solução completaQuestão 87
Um líquido escoa da esquerda para a direita no cano mostrado na figura. Os pontos A e B estão na mesma altura, mas a área da seção reta do cano é diferente nos dois pontos. Os pontos B e C estão em alturas diferentes, mas a área da seção reta do cano é igual nos dois pontos. Indique a relação correta entre as pressões nos três pontos.

Questão 88
De um grande recipiente fechado para a atmosfera escoa água continuamente por um cano aberto, como podemos ver na figura. A altura do ponto 1 é e a dos pontos 2 e 3 é . A área transversal no ponto 2 e no ponto 3 é . A área transversal do recipiente é muito grande comparada com as áreas transversais do cano. Para simplificar, suponha e . A densidade da água é . Sabendo-se que num dado instante a velocidade do líquido no ponto 3 vale , calcule:
a) A pressão do ar retido na parte superior do reservatório.
b) A velocidade e a pressão no ponto 2.
c) A vazão volumétrica neste instante.
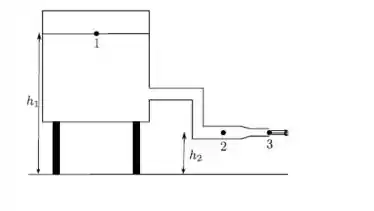
Questão 89
Considere um tubo horizontal cuja seção reta diminui ao longo do seu comprimento. Se um fluido incompressível estiver escoando da seção larga para a estreita, então:
- A velocidade e a pressão diminuirão.
- A velocidade diminuirá, mas a pressão aumentará.
- A velocidade aumentará, mas a pressão diminuirá.
- A velocidade e a pressão aumentarão.
- A velocidade OU a pressão se modificará, mas não ambas.
Questão 90
Num túnel de vento para testes aerodinâmicos um fluxo estacionário de ar é estabelecido em torno de um protótipo de asa delgado. O formato da asa é tal que a razão entre a velocidade do ar na parte superior, , e sua velocidade na parte inferior, , vale . Sendo a área da asa, a sua massa, e considerando o ar um fluido incompressível ideal de densidade , a velocidade mínima para que a asa seja sustentada por este fluxo de ar vale:
Questão 91
Em uma indústria química, álcool (Etanol) com densidade , escoa em regime laminar por um tubo cuja geometria é mostrada na figura. O líquido manométrico é o mercúrio e a diferença de altura determina a diferença de pressão entre os dois setores do escoamento.
a) Determine a diferença de pressão em atmosferas.
b) Determine a vazão do etanol sabendo que
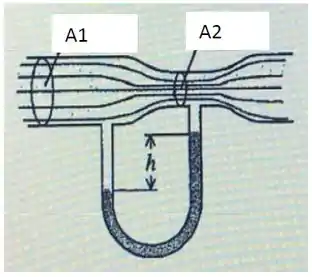
Questão 92
A água flui no cano mostrado abaixo com velocidade de
- Qual é a velocidade do fluido na seção do cano logo abaixo da coluna aberta?
- Qual é a pressão da água imediatamente ao sair para o ar?
- Qual é a altura da coluna de água?
Questão 93
Um fluido incompressível passa com velocidade por uma tubulação cuja seção transversal possui área num dado ponto inicial . Em um outro ponto da tubulação, com uma altura acima do ponto inicial, a velocidade do fluido é e a pressão é exatamente igual àquela do ponto . Tome . Considere as afirmações:
Como a pressão é a mesma nos dois pontos, então para compensar a diferença de altura entre e .
A área da seção transversal no ponto é o triplo de .
A vazão na tubulação nos ponto e é a mesma.
Dentre as afirmações acima a(s) correta(s) é(são):
Todas
Ver solução completa