Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 32.10 - Ex. 45
Considere um sólido com átomos por unidade de volume, cada átomo com um momento dipolar magnético . Suponha que existam apenas duas orientações possíveis para : paralelo ou antiparalelo a um campo magnético externamente aplicado (o que, segundo a física quântica, acontece quando apenas um elétron do átomo é responsável pelo spin ). De acordo com a mecânica estatística, a probabilidade de que um átomo se encontre em um estado de energia é proporcional a , onde é a temperatura e é a constante de Boltzman. Assim, como a energia é igual a , a fração de átomos com o momento dipolar paralelo a é proporcional a e a fração de átomos com o momento dipolar antiparalelo a é proporcional a . (a) Mostre que o módulo da magnetização do sólido é , onde . (b) Mostre que o resultado do item (a) se reduz a para . (c) Mostre que o resultado do item (a) se reduz a para . (d) Mostre que (b) e (c) concordam qualitativamente com a Fig. 32-14.
Passo 1
Esse é um dos problemas que os físicos mais gostam de resolver: trata-se de um dos principais problemas da mecânica estatística e seu resultado é bem bonitinho e pode ser obtido de uma forma relativamente simples...
Imagine que metade das partículas () tem spin e a outra metade tem spin . Assim, a soma dos spins será:
Por outro lado, se tivermos partículas com spin e com spin :
A magnetização média de um spin será a soma dos spins dividida pelo número total de partículas :
Passo 2
O número de partículas será proporcional a probabilidade de ocorrência daquele estado, de modo que podemos fazer a substituição:
Assim,
Por fim, a magnetização total do sistema será a magnetização por átomo vezes o número de átomos:
Passo 3
Para o item (b) vamos ter que lembrar que para :
Assim,
Portanto, neste limite
Note que essa basicamente é a lei de Curie e vale para pequeno (é muito bonitinho, eu sei)!
Passo 4
Para o item (c), lembre-se que para muito grande, temos que , de modo que
Assim, no limite , temos que
Assim, vemos que para grandes , a magnetização se aproxima de uma constante, isto é, tem uma assíntota no infinito.
Passo 5
Note que nos dois limites (itens (b) e (c)), obtivemos, respectivamente:
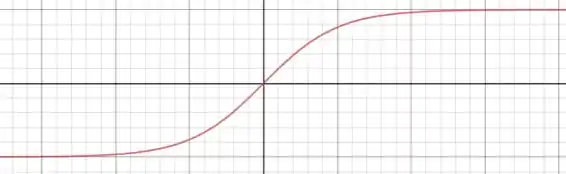
Para baixos valores de , o comportamento da curva de magnetização é linear. Já para grandes, o comportamento deixa de ser linear e a curva se aproxima de uma assíntota. Este é exatamente o comportamento da curva da Fig. 32-14. A seguir fazemos um esboço de uma curva de magnetização:
Resposta
Demonstração.