Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 12.1 - Ex. 59
Considere uma viga rígida de 2,5 m de comprimento (Figura 12-51), suportada em seu centro no topo de um poste fixo de 1,25 m de altura, podendo pivotar sobre um mancal sem atrito. Uma extremidade da viga está ligada ao chão por uma mola com a constante de força Quando a viga está na horizontal, a mola fica frouxa e na vertical. Se um objeto pendurado na outra extremidade da viga, esta atinge uma posição de equilíbrio formando um ângulo de 17,5° com a horizontal. Qual é a massa do objeto?
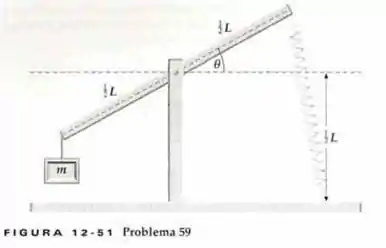
Passo 1
Bom, aqui temos uma barra em equilíbrio conectada a uma mola. Quando adicionamos um corpo de massa m ao outro lado da barra, ela vai girar e atingir novamente o equilíbrio.
Vocês podem se perguntar, isso muda alguma coisa? Não ! As condições do equilíbrio também são válidas aqui, ou seja:
Agora vamos desenhar esta situação, colocando as forças que atuam sobre esta placa:
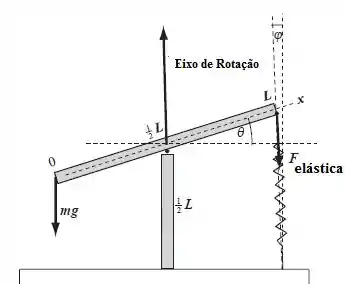
Onde o corpo está pendurado, temos a força gravitacional sendo aplicada para baixo. Dada por:
Temos a força normal, na direção do nosso eixo de rotação. E a força elástica exercida pela mola, dada por:
O eixo x é dado na direção da placa, como podemos ver na figura. Sendo assim, tanto a força peso quanto a elástica formam um ângulo diferente de 90° com a placa. Para conseguir realizar o torque precisamos das forças perpendiculares à placa, neste caso e .
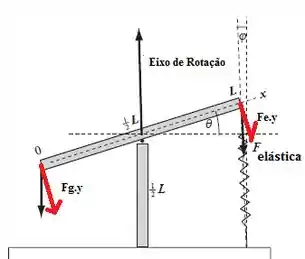
Para a Força Peso, usamos a trigonometria para descobrir que o ângulo entre vale e formam um triângulo retângulo.
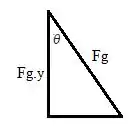
Sendo assim:
Esse foi fácil né ?! Mas para a força elástica vai ser um pouco mais confuso. Então vamos com muita calma.
A mola, na posição inicial estava na vertical formando um ângulo de 90° com posição inicial da barra. Quando a mola é esticada, ela se desloca para a esquerda formando um ângulo com sua posição inicial. Quando acrescentamos a força na direção y formamos um triângulo obtuso. Amplificando o desenho para a Força elástica:
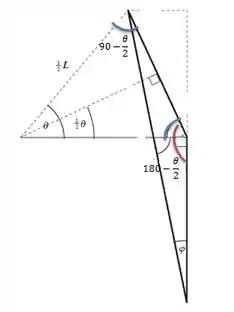
Pela lei dos senos:
Pela identidade:
Substituímos os valores:
Calma pessoas ! Vamos mexer mais um pouco nesse seno usando outra identidade:
Por trigonometria:
Usando a regra dos cossenos:
Concluímos que:
Substituímos na identidade:
Resolvemos por Báskara:
Escolhemos o valor positivo, já que temos um ângulo agudo.
Ufa ! Agoraa sim vamos conseguir calcular
Beleza! Agora só precisamos fazer o somatório dos torques.
Passo 2
O torque é calculado como:
Onde r é a distância entre a força e o eixo de rotação, então para ambas as forças Quando fazemos isso:
Substituindo e
Substituindo e
Isolando m
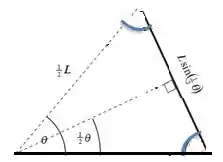
A trigonometria nos ajuda a descobrir os catetos do triângulo retângulo, já que temos a hipotenusa e um ângulo:
Então:
Lembrando que
Na equação para a massa:
Sabendo que
Nos resta apenas saber quanto a mola se esticou,
Passo 3
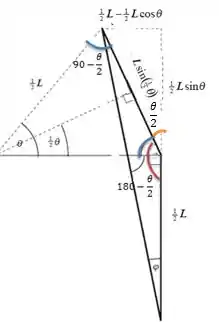
Cansativo né?! Mas estamos acabando, só precisamos achar , que vai ser:
No desenho vemos que tem o comprimento da parede:
Pela figura anterior podemos ver que é o lado oposto ao ângulo Vamos aplicar novamente a Lei dos cossenos no triângulo formado pela mola:
Usando a fórmula do cosseno para a diferença de dois ângulos:
Lembrando de duas identidades:
Substituímos:
Sabendo que
Calma que não acabou...
Passo 4
Agora que temos todos os valores, vamos colocar na massa: