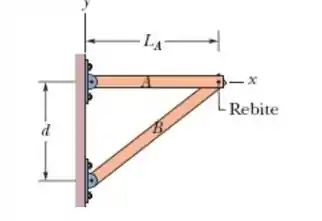
Na Figura, vigas homogêneas e estão presas a uma parede por dobradiças e frouxamente rebitadas uma na outra (uma não exerce torque sobre a outra). A viga tem comprimento e massa de ; a viga tem massa de . As dobradiças estão separadas por uma distância . Na notação dos vetores unitários, qual é a força (a) sobre a viga A exercida por sua dobradiça, (b) sobre a viga A exercida pelo rebite, (c) sobre a viga B exercida por sua dobradiça e (d) sobre a viga B exercida pelo rebite?

Considerando agora somente a viga e igualando a zero a soma dos torques com relação ao rebite, temos:

Podemos escrever a foca que a dobradiça exerce sobre na forma de vetores unitários:

(b) Das equações de equilíbrio da viga , sendo a força exercida pelo rebite em , temos:

Então,

(c)Considerando o sistema viga +viga como somente um, sendo a força exercida pelo rebite sobre , temos:

Então,

(d)Pela terceira lei de Newton, a força exercida pelo rebite sobre é dada por