Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 12.2 - Ex. 39
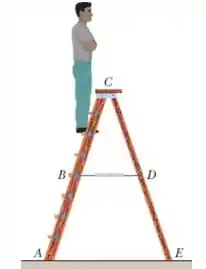
Os lados e da escada da figura têm de comprimento e estão unidos por uma dobradiça no ponto . A barra horizontal tem de comprimento e está na metade da altura da escada. Um homem que pesa sobe ao longo da escada. Supondo que não há atrito com o piso e desprezando a massa da escada, determine (a) a tensão da barra e o módulo da força que o chão exerce sobre a escada (b) no ponto A e (c) no ponto E. (Sugestão: Isole partes da escada ao aplicar as condições de equilíbrio.)
Passo 1
Show de bolinhas pessoal, primeiro a gente pode considerar o diagrama de corpo livre de cada parte da escada, como na figura a seguir:
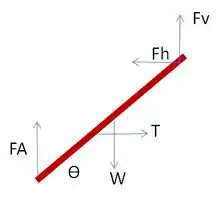
e são forças exercidas pelo piso, é o peso do homem, a componente horizontal da força exercida por um dos lados da escada sobre o outro e a força vertical, componetne da mesma força.
Passo 2
Como a escada está em equilíbrio:
Como o torque é nulo também, temos:
Passo 3
Analisando o lado direito, temos:
Passo 4
O problema nos dá um sistema de 5 equações e 5 incógnitas ( Realizando as devidas substituições, conseguimos encontrar
Para encontrar , devemos usar as relações geométricas do problema. Nesse caso, podemos notar, no triângulo formado por metade da barra, que
Então:
Passo 5
(b)Para acharmos , vamos usar a equação
Passo 6
(c)Aqui, sai diretamente da expressão