Para construir uma escultura móvel, um artista pendura uma esfera de alumínio de de massa presa a um fio de aço da de comprimento com área da seção reta igual a . À parte inferior da esfera ele prende outro fio de aço semelhante, na extremidade do qual ele pendura um cubo de bronze de massa igual a . Para cada fio, calcule a) tensão de dilatação; b) o alongamento.

Precisamos usar a primeira condição de equilíbrio para calcular as tensões e e o alongamento de cada fio:

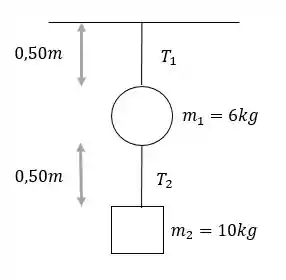
Agora vamos esboçar um diagrama de corpo livre apenas da massa e usar a equação do equilíbrio de forças nela:

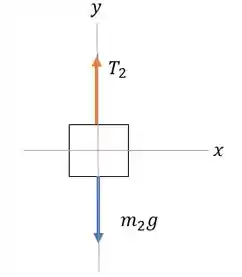
Somando as forças verticais, temos:

E encontramos uma das tensões:

Fazendo o mesmo para :

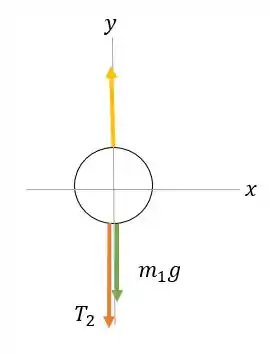
E somando as forças verticais:

Obtemos o valor da outra tensão no fio:

Agora, calcularemos a tensão de dilatação no fio usando a fórmula do módulo de Yong:

Então,

Para o fio superior, vamos ter:

E substituindo os valores dados, temos:

Agora para o fio inferior, vamos fazer a mesma coisa, substituindo os valores do enunciado:

E obtemos:

Na letra (b), calcularemos o alongamento usando a relação:

Então,

Sendo assim, usando o valor encontrado no passo anterior, vamos ter para o fio inferior:

E para o fio superior:

Isso significa que a tensão é maior no fio superior, porque ele deve suportar os dois objetos. Os fios têm o mesmo comprimento e diâmetro, então aquele com maior tensão tem maior tensão e alongamento.

Valeu, galera! Até a próxima! 😉