Enunciado
Física - Príncipios de física - Serway - Princípios De Física: Mecânica Clássica e Relatividade - Ed: 5º - Capítulo 10.Problemas - Ex. 28
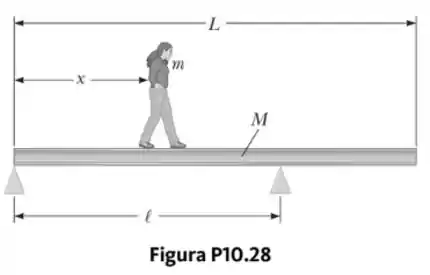
Uma viga uniforme repousando em dois pinos tem comprimento e massa . O pino à esquerda exerce uma força normal sobre a viga, e o outro, localizado a uma distância da extremidade esquerda, exerce uma força normal . Uma mulher de massa pisa na extremidade esquerda da viga e começa a caminhar para a direita, como na Figura P10.28. O objetivo é encontrar a posição da mulher quando a viga começa a inclinar.
- Qual é o modelo de análise apropriado para a viga antes de começar a inclinar?
- Esboce um diagrama de força para a viga, rotulando as forças gravitacionais e normais agindo sobre ela e posicionando a mulher a uma distância à direita do primeiro pino, que é a origem.
- Onde está a mulher quando a força normal é maior?
- Qual é quando a viga está prestes a inclinar?
- Use a Equação 10.27 para encontrar o valor de quando a viga está prestes a inclinar.
- Usando o resultado da parte (d) e a Equação 10.28, com torques calculados em torno do segundo pino, encontre a posição da mulher quando a viga está prestes a inclinar.
- Verifique a resposta para a parte (e) calculando os torques em torno do ponto do primeiro pino.
Passo 1
E aiii gente, tudo bem com vocês?
Vamos fazer uma questãozinha aqui?
Vem comigo!
Letra a:
Objeto rígido em equilíbrio estático.
Passo 2
Letra b:
Passo 3
Letra c:
Observe que sobre o pivô direito, apenas exerce um torque no sentido horário, todas as outras forças exercem torques no sentido anti-horário, exceto para que exerce torque zero. A mulher está em x = 0 quando é o maior.
Com esta localização da mulher, o torque anti-horário sobre o centro da viga é um máximo. Assim, deve estar exercendo seu torque máximo no sentido horário sobre o centro para segura a viga em equilíbrio rotacional.
Passo 4
Letra d:
Enquanto a mulher caminha para a direita ao longo da viga, ela eventualmente chega a um ponto a viga começa a rotacionar no sentido horário sobre o pivô mais à direita. Neste ponto, a viga está começando a levantar do pivô mais à esquerda e a força normal exercido por esse pivô terá diminuído para zero.
Passo 5
Letra e:
Quando a viga está inclinar , e:
Passo 6
Letra f:
Exigindo que o torque líquido seja zero sobre o pivô correto quando a viga está prestes a inclinar nos dá:
Passo 7
Letra g:
Quando , para torque sobre o pivô esquerdo:
Resposta
- Objeto rígido em equilíbrio estático.
- A mulher está em x = 0 quando é o maior.