Enunciado
Física - Príncipios de física - Serway - Princípios De Física: Mecânica Clássica e Relatividade - Ed: 5º - Capítulo 10.Problemas - Ex. 32
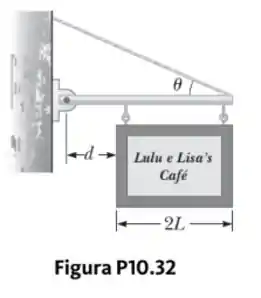
Uma placa uniforme de peso e largura está pendurada em uma viga horizontal leve presa à parede e suportada por um cabo (Fig. P10.32). Determine
- a tensão no cabo e
- as componentes da força de reação exercida pela parede na viga quanto a , , e .
Passo 1
E aiii gente, tudo bem com vocês?
Vamos fazer uma questãozinha aqui?
Vem comigo!
Sabemos que a direção da força do cabo na extremidade direita está ao longo do cabo, em um ângulo de acima da horizontal. Na outra ponta, não sabemos magnitude ou direção para a força de dobradiça , então nós o mostramos como dois componentes desconhecidos.
A primeira condição para equilíbrio nos dá duas equações:
Tomando torques sobre a extremidade esquerda, descobrimos que a segunda condição é:
Passo 2
Letra a:
A equação de torque nos dá:
Passo 3
Letra b:
Das equações de força:
Resposta
Exercícios de Livros Relacionados
Uma demonstração comum, ilustrada na Figura P10.76, consiste em uma bola repousando em uma extremidade de uma mesa uniforme de comprimento l que é presa na outra extremidade e elevada a um ângulo de θ
Suponha que uma pessoa se incline para a frente para levantar um peso “com suas costas”, como mostrado na Figura P10.79a. A coluna vertebral gira principalmente na quinta vértebra lombar com a força d
Uma escada portátil de peso desprezível é construída como mostrado na Figura P10.73, com A C=B C=l=4,00m . Um pintor de massa m=70,0k g sobe na escada d=3,00m do chão. Considerando o piso sem atrito,
A Figura P10.82 mostra uma força vertical aplicada tangencialmente a um cilindro uniforme de peso F g . O coeficiente de atrito estático ente o cilindro e todas as superfícies é 0,500 . A força P → é
Uma bobina oca, cilíndrica e uniforme tem raio interno R / 2 , raio externo R e massa M (Fig. P10.70). Ela é montada de modo a girar em um eixo horizontal fixo. Um contrapeso de massam é conectado à p