Enunciado
Física - Príncipios de física - Serway - Princípios De Física: Mecânica Clássica e Relatividade - Ed: 5º - Capítulo 4.Problemas - Ex. 54
Um corpo de desliza por um plano inclinado fixo, sem atrito. Use um computador para determinar e tabular
- a força normal exercida sobre o corpo e
- sua aceleração para uma série de ângulos de inclinação do plano (medidos a partir da horizontal) variando de a em incrementos de .
- Trace um gráfico da força normal e da aceleração em função do ângulo de inclinação.
- Nos casos limites de e , seus resultados são coerentes com o comportamento conhecido?
Passo 1
E aiii galera, vamos fazer mais uma questão aqui?
Vem comigo!
Aplicando a segunda Lei de Newton na direção x, temos:
E na direção y:
Abaixo, um esquema para facilitar a compreensão:
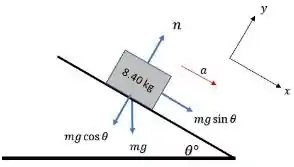
Passo 2
Letra a e b:
Para a letra a e b usamos MatLab para construir os gráficos e chegar nas respostas
Passo 3
Letra c:
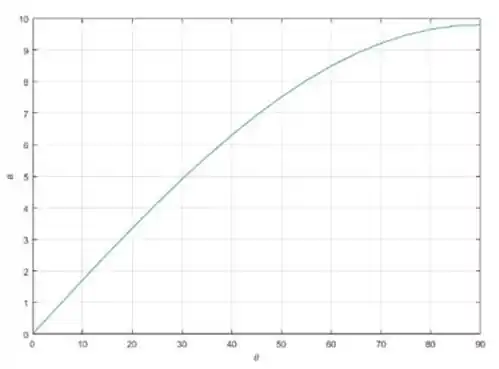
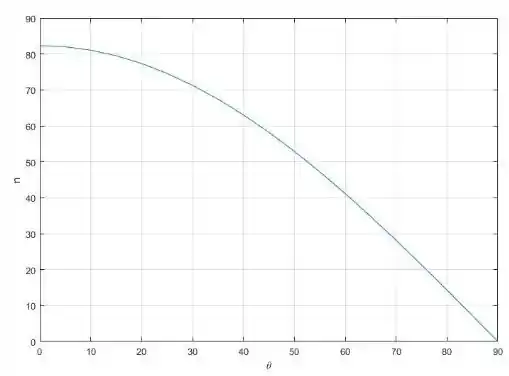
Passo 4
Letra d:
Quando , o peso total é para baixo e não há nenhuma força horizontal para colocar o bloco em movimento, então , e o peso é perpendicular à superfície, então a força normal é igual ao peso total
Quando o bloco está em queda livre , e não há contato com a superfície, então n=0
Resposta
- Ver resolução
- Ver resolução
- Ver resolução
- Quando , o peso total é para baixo e não há nenhuma força horizontal para colocar o bloco em movimento, então , e o peso é perpendicular à superfície, então a força normal é igual ao peso total
Quando o bloco está em queda livre , e não há contato com a superfície, então n=0