Enunciado
Física - Curso de Física Básica - Mecânica Volume 1 - 5ª Edição - Herch Moysés Nussenzveig- Ed: 5º - Capítulo 4.Problemas - Ex. 9
Um automóvel estacionado no alto de uma ladeira molhada pela chuva, de 100 m de comprimento e 25m de altura, perde os freios e desliza pela ladeira( despreze o atrito ). Com que velocidade, em km/h, ele atinge o pé da ladeira?
Passo 1
Bom galera, a primeira coisa que podemos fazer aqui é imaginar essa ladeira como um triângulo retângulo, assim a gente descobre que parcela da gravidade atua acelerando o carro!
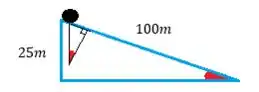
(vamos chamar nosso ângulo vermelho de )
Como sabemos, a gravidade está na direção da hipotenusa daquele triangulo pequeno e a componente que queremos encontrar está na direção da ladeira. Se observarmos bem, aquele ângulo que toca a bolinha preta é o mesmo que está no topo da ladeira, então temos triângulos semelhantes aí !
Bom, como queremos o cateto oposto da gravidade nossa aceleração fica , mas sabemos do triângulo maior que . Então temos
Passo 2
Para sabermos a velcidade final usamos torricelli de novo já que não temos o tempo.