Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 4.1 - Ex. 90

Uma superfície sem atrito está inclinada de um ângulo de 30,0 ° com a horizontal. Um bloco de 270   g , sobre a rampa, é amarrado a um bloco de 75,0   g , usando-se uma polia, como mostra a Figura 4-62. (a) Desenhe dois diagramas de corpo livre, um para o bloco de 270   g e outro para o bloco de 75,0   g . (b) Encontre a tensão no fio e a aceleração do bloco de 270   g . (c) O bloco de 270 g é largado do repouso. Quanto tempo leva para ele deslizar uma distância de 1,00   m   ao longo da superfície? Ele deslizará para cima ou para baixo do plano inclinado?

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Os diagramas de corpo livre dos blocos de 270   g e 75   g estão expostos abaixo:

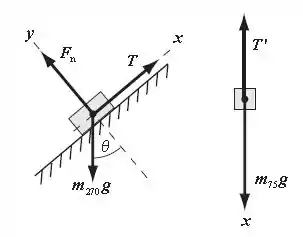
Passo 2

Item (b):

Aplicando ∑ F → = m a → , para cada bloco, temos:

∑ F x = m a x

T - m 270 g sin ⁡ θ = m 270 a 1 x

m 75 g - T = m 75 a 2 x

Como os corpos estão conectados por uma polia simples, as suas acelerações serão iguais, portanto podemos relacionar as equações, isolando T :

m 75 g - m 75 a = m 270 g sin ⁡ θ + m 270 a

a = m 75 - m 270 sin ⁡ θ g m 270 + m 75

Substituindo os valores, temos:

a = 75 - 270 sin ⁡ 30 ° ( 9,81   m / s 2 ) 270 + 75

a = - 1,706   m / s 2

A tensão será:

T = m 75 g - m 75 a

T = ( 0,075   k g ) ( 9,81 m / s 2 - ( - 1,706   m / s 2 ) )

T = 0,864   N

Passo 3

Para o item (c), podemos usar a equação da posição para aceleração constante para encontrar o tempo.

∆ x = v 0 x ∆ t + 1 2 a x ∆ t 2

Como o corpo parte do repouso, sua velocidade inicial é nula, logo:

∆ x = 1 2 a x ∆ t 2

∆ t = 2 ∆ x a x

Substituindo os valores, temos:

∆ t = 2 ⋅ ( - 1   m ) - 1,706   m / s 2

∆ t = 1,08   s

Resposta

b )   a = - 1,706   m / s 2

T = 0,864   N

c ) ∆ t = 1,08   s

O corpo vai para baixo pois sua aceleração é negativa, ou seja, no sentido de descida da rampa.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um bloco começa a subir um plano inclinado sem atrito com uma velocidade inicial v 0 = 3,50m / s . O ângulo do plano inclinado é θ = 32,0 ° . (a) Que distância ao longo do plano inclinado o bloco cons
Na Fig. 5-40, um caixote de massa m = 100k g é empurrado por uma força horizontal F → que o faz subir uma rampa sem atrito ( θ = 30,0 ° ) com velocidade constante. Quais são os módulos (a) de F → e (b
Um esquiador de 40k g desce uma rampa sem atrito que faz um ângulo de 10 ° com a horizontal. Suponha que o esquiador se desloca no sentido negativo de um eixo x orientado ao longo da rampa. O vento ex
Uma cunha de massa M repousa sobre o topo horizontal de uma mesa sem atrito. Um bloco de massa m é colocado sobre a cunha (Figura P5.112a). Não existe nenhum atrito entre o bloco e cunha. O sistema é
Uma cunha de massa M repousa sobre o topo horizontal de uma mesa sem atrito. Um bloco de massa m é colocado sobre a cunha e uma força horizontal F é aplicada sobre ela (Figura P5.112b). Qual deve ser