Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 4.Exercícios e Problemas - Ex. 86
Correndo o perigo de afundar no rio, uma criança está sendo levada pela correnteza, que flui uniformemente a . A criança encontra-se a da margem e rio acima do trapiche de onde uma equipe de resgate sai em seu socorro. Se o barco da equipe desloca-se com relação à água, em que ângulo com a margem do rio o piloto deve orientar o barco a fim de ir diretamente até a criança?
Passo 1
Bom, o problema envolve velocidades relativas, a correnteza do rio se move a enquanto o barco se move em relação ao rio, o que significa que a velocidade do barco para quem está olhando da margem é:
Sendo que é a velocidade do barco em relação à margem e é a velocidade do barco em relação ao rio.
Tirando o módulo:
Substituindo os valores:
Esse vai ser o módulo da velocidade do barco em relação à margem, vamos chamar ela de .
Passo 2
Vamos dar uma olhada no seguinte esquema:
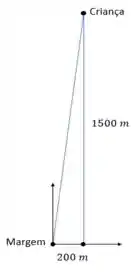
Como dá para ver, a criança começa seu movimento em e , mas não sabemos a posição final dela, que será quando a equipe de resgate vai chegar. Vamos então escrever a equação de movimento para a criança no eixo :
Passo 3
O deve ser o mesmo para a equipe de resgate, e o da equipe de resgate deve ser igual a . As equações do eixo e do eixo para o barco da equipe vão ser:
Como a margem está na vertical, o cosseno da velocidade do barco em relação à margem que vai dar a componente da velocidade.
Igualando as equações em
Mas não temos o tempo, que será igual para os dois, já que queremos que o barco chegue na criança, vamos isolar ele na equação de para fazer ele sumir:
Substituindo:
Vamos multiplicar toda a equação por :
E isolar de um lado tudo que envolve :
Tirando fator comum e passando ele dividindo:
Resolvendo a equação em relação a :