Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 4.Exercícios e Problemas - Ex. 46
Um jogador de tênis rebate a bola 2,0 m acima do piso. A bola sai da raquete com rapidez de 20,0 m/s, formando um ângulo de 5,0° acima da horizontal. A distância horizontal até a rede é de 7,0 m, e esta tem 1,0 m de altura. A bola ultrapassará a rede? Em caso afirmativo, em quanto? Em caso negativo, quanto faltou para isso?
Passo 1
O exercício nos dá
E o que ele quer saber
E o esqueminha do movimento é
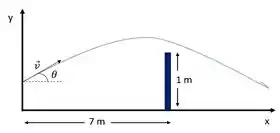
Passo 2
A velocidade em relação ao e ao é
Assim, em relação a é Movimento Uniforme, logo podemos usar
Substituindo o tempo na equação em , que é um Movimento Uniformemente Variado
Resposta
Sim, a bola ultrapassa a rede com de diferença
Exercícios de Livros Relacionados
Na Fig. 4-40, uma bola é lançada com uma velocidade de 10,0m / s e um ângulo de 50,0 ° com a horizontal. O ponto de lançamento fica na base de uma rampa de comprimento horizontal d 1=6,00m e altura d
Na Fig. 4-41, uma bola é arremessada para o alto de um edifício, caindo 4,00s depois a uma altura h=20,0m acima da altura de lançamento. A trajetória da bola no final da trajetória tem uma inclinação
Uma bola é lançada do solo em direção a uma parede que está a uma distânciax (Fig. 4-43a). A Fig. 4-43b mostra a componente v y da velocidade da bola no instante em que alcançaria a parede em função d
O chute de um jogador de futebol americano imprime à bola uma velocidade inicial de 25m / s . Quais são (a) o menor e (b) o maior ângulo de elevação que ele pode imprimir à bola para marcar um field g
Os esquiadores experientes costumam dar um pequeno salto antes de chegarem a uma encosta descendente. Considere um salto no qual a velocidade inicial é v 0 =10m / s , o ângulo é θ 0 =9,0 ° , a pista a