Exercícios de Lançamento Oblíquo - Lista de Exercícios Resolvida
Questão 1
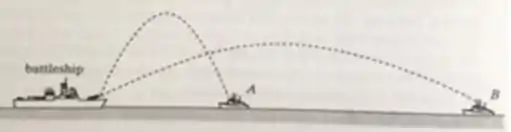
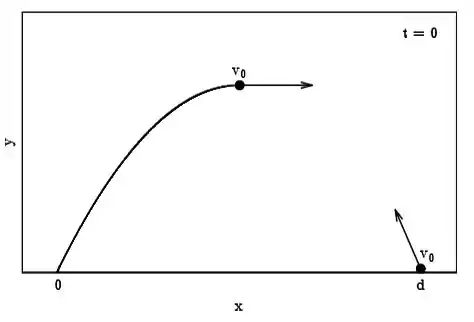
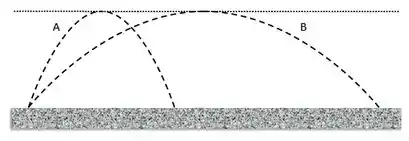
Um navio de guerra tenta bombardear simultaneamente dois navios A e B. Se os projéteis são disparados com velocidades cujas magnitudes são idênticas e seguem as trajetórias mostradas na figura abaixo, qual dos navios é atingido primeiramente? Despreze a resistência do ar
A.
B.
Os dois são atingidos simultaneamente.
Mais informação é necessária para se responder esta questão.
Nenhuma das alternativas é correta
Ver solução completaQuestão 2
Um canhão lança suas balas com uma certa inclinação em relação à horizontal. Assuma que a bala atinge o chão na mesma elevação em que foi lançada.
Se o tempo de voo foi de segundos, qual a componente vertical de sua velocidade inicial?
(Considere )
50
nenhuma das anteriores
Ver solução completaQuestão 3
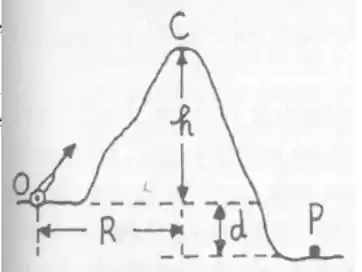
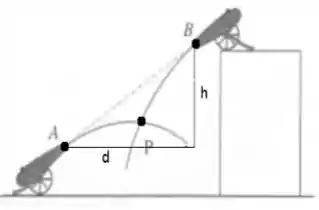
Dois canhões apontam-se mutuamente, como mostrado na figura, e disparam suas balas no mesmo instante de tempo. O canhão dispara sua bala com velocidade de módulo , e o canhão com velocidade . As distâncias no problema são .
Qual a aceleração de cada uma das balas após o disparo?
Quanto tempo se passou a partir do momento do disparo até o instante da colisão? A que altura acontece a colisão?
Se não houvesse o canhão , qual seria o alcance da bala do canhão A?
Ver solução completaQuestão 4
Um projétil é lançado do nível do chão com uma rapidez inicial de . Encontre o ângulo de lançamento ( o ângulo que a velocidade inicial forma acima da horizontal) de forma que a altura máxima do projétil seja igual ao seu alcance horizontal. (Ignore a resistência do ar.)
Ver solução completaQuestão 5
Você assiste seu amigo jogando hóquei. Durante o jogo, ele atinge o disco de tal forma que, ao chegar no seu ponto mais alto, o disco passa de raspão por cima do muro de acrílico de de altura que cerca o campo, distante do jogador. Encontre a componente vertical da velocidade inicial, o tempo para atingir o muro e a componente horizontal da velocidade inicial, a rapidez inicial e o ângulo de lançamento. (Ignore a resitência do ar.)
Ver solução completaQuestão 6
Um canhão, posicionado sobre um terreno completamente plano, dispara um projétil com um velocidade inicial de módulo fazendo um ângulo de com a horizontal. Considerando a posição incial do canhão como origem do sistema de coordenadas e a aceleração da gravidade determine:
O tempo total de voo do projétil.
O vetor posição do projétil quando o mesmo atinge sua altura máxima.
O vetor velocidade quando o mesmo atinge o solo.
Considere agora que o projétil deva atingir um alvo que está a uma distância de do canhão. Qual deve ser o ângulo de tiro para que o projétil com velocidade inicial de módulo possa atingir o alvo?
Ver solução completaQuestão 7
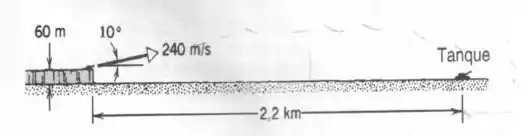
Um certo avião tem uma velocidade de e está mergulhando com um ângulo abaixo da horizontal quando o piloto libera um chamariz. A distância horizontal entre o ponto de lançamento e o ponto onde o chamariz se choca com o solo é . Quanto tempo o chamariz passou no ar? De que altura foi lançado?
Questão 8
Um jogador de futebol bate uma falta, fazendo com que a bola saia com velocidade inicial , do solo, fazendo um ângulo de . Sabendo que um vento sopra da esquerda para direita, imprimindo uma aceleração nessa direção com módulo igual ao módulo da gravidade. Determine a altura máxima do chute, e seu alcance. Na frente do jogador, a , está um gol com de altura. Determine se a bola vai na direção do gol, passa por cima dele, ou cai antes do gol.
Dados: , 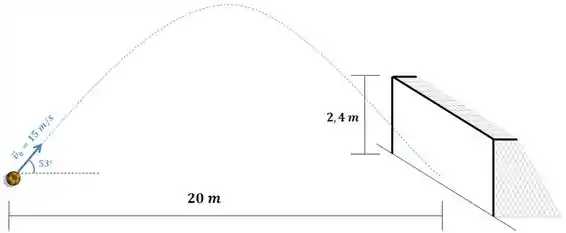
Questão 9
Um projétil é lançado com velocidade formando um ângulo com a horizontal. O ponto de lançamento está localizado a uma altura acima do solo. A figura mostra o sistema de referencia fixo, que está localizado no solo e tem eixo vertical alinhado verticalmente com o ponto de lançamento. De acordo com este referencial, pressupondo que a resistência do ar é desprezível e que a Terra é um referencial Inercial:
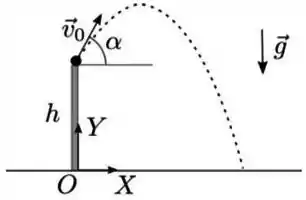
Escreve os vetores posição e velocidade , como funções do tempo , usando os unitários e dos eixos e , respectivamente, indicados na figura;
Calcule o tempo que o projétil leva para atingir a altura máxima;
Calcule o tempo de vôo do projétil.
Determine, quando o projétil toca o solo, o módulo da sua velocidade .
Ver solução completaQuestão 10
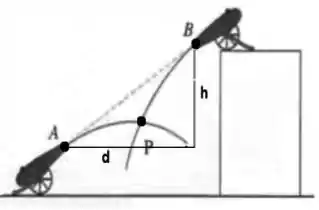
Darlene é uma motociclista de circo. Como clímax de seu show, ela larga de uma rampa inclinada de , salta um fosso de largura e pousa em um rampa mais elevada (altura ) do outro lado . Para uma dada altura , encontre a mínima rapidez de largada necessária para ela realizar o salto com sucesso. Quanto vale para , e ?
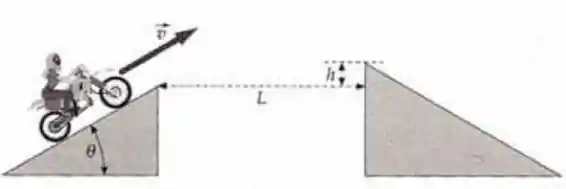
Mostre que, independente da rapidez de largada, a altura máxima da plataforma é . Interprete fisicamente este resultado. (Despreze a resistência do ar e trate a motoqueira e a moto como se fossem uma única partícula.)
Ver solução completaQuestão 11
Um mergulhador salta de um penhasco em Acapulco, no México, acima da superfície da água. Neste momento, ele aciona sua mochila-foguete horizontamente, o que lhe dá uma aceleração horizontal constante de , sem efetuar seu movimento vertical. Quanto tempo ele leva até chegar à superfície da água? A que distância da base do penhasco ele atinge a água, suponto o penhasco vertical? Mostre que sua trajetória é uma linha reta. (Ignore a resistência do ar.)
Ver solução completaQuestão 12
Uma partícula é lançada de uma catapulta no instante , com uma velocidade inicial de módulo e um ângulo de acima da horizontal. Quais são os módulos das componentes horizontal e vertical do deslocamento da pedra em relação à catapulta em ? Repita os cálculos para as componentes horizontal e vertical em e para as componentes horizontal e vertical em .
Dados:
Ver solução completaQuestão 13
Uma bola de futebol é chutada a partir do chão com uma velocidade inicial de e um ângulo para cima de . No mesmo instante um jogador a de distância, na direção do chute, começa a correr para receber a bola. Qual deve ser sua velocidade média para que alcance a bola imediatamente antes que toque o gramado?
Ver solução completaQuestão 14
Ao ser disparado verticalmente um projétil atinge uma altura máxima . Se o mesmo projétil é disparado numa direçãoo que faz ângulo com a horizontal, a altura máxima atingida é igual a:
Questão 15
Dois projéteis 1 e 2 são lançados simultaneamente e horizontalmente de alturas e (diferentes) em relação ao solo. Verifica-se que ambos atingem o mesmo ponto no solo e têm o mesmo alcance . A razão entre os módulos e das velocidades de lançamento dos respectivos projéteis 1 e 2 é
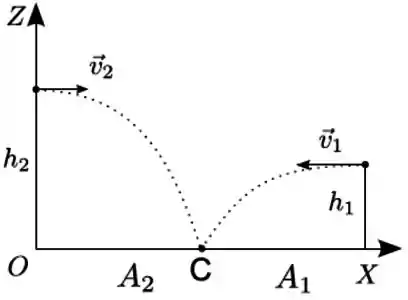
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 16
[1] Uma bola de beisebol é golpeada a uma altura e apanhada na mesma altura, conforme a figura. Deslocando-se paralelamente a um muro, ela passa pelo alto do muro após ter sido golpeada e, novamente, depois quando está descendo, em posições separadas por uma distância
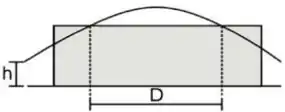
(a) Escolha um sistema de coordenadas e escreva o vetor velocidade inicial da bola imediatamente após ela ter sido golpeada. Qual o ângulo que faz com a horizontal?
Ver solução completaQuestão 17
[1] Uma bola de beisebol é golpeada a uma altura e apanhada na mesma altura, conforme a figura. Deslocando-se paralelamente a um muro, ela passa pelo alto do muro após ter sido golpeada e, novamente, depois quando está descendo, em posições separadas por uma distância
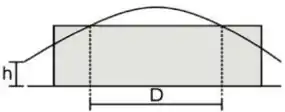
(c) Qual a distância horizontal percorrida pela bola do instante em que foi golpeada até ser apanhada?
Ver solução completaQuestão 18
[1] Uma bola de beisebol é golpeada a uma altura e apanhada na mesma altura, conforme a figura. Deslocando-se paralelamente a um muro, ela passa pelo alto do muro após ter sido golpeada e, novamente, depois quando está descendo, em posições separadas por uma distância
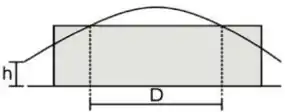
(b) Qual é a altura do muro e qual é o alcance vertical máximo da bola?
Ver solução completaQuestão 19
Um foguete é lançado de um ângulo do topo de uma torre com altura . Devido ao design das engrenagens, suas coordenadas são da forma e onde e são constantes. Além disso, a aceleração do foguete após o lançamento é . Use a origem do eixo de coordenadas como a base da torre.
(a) Encontre as constantes e , incluindo suas unidades do SI.
Ver solução completaQuestão 20
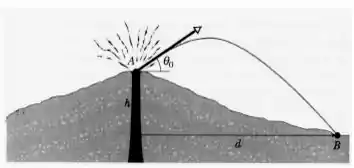
Um cineasta filma a erupção de um vulcão e, num certo instante, ele registra um bloco sendo arremessado fazendo um ângulo com a horizontal, partindo da boca do vulcão de uma altura a partir do solo. Ele acompanha o movimento do bloco e o filma batendo no solo, como na figura, um tempo após ser lançado. Desprezando a resistência do ar,
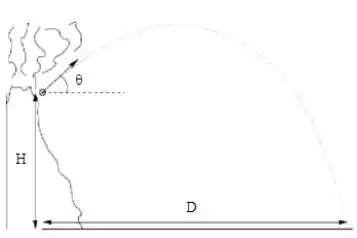
- Calcule a distância horizontal que o bloco percorreu do instante em que foi arremessado da boca do vulcão até o momento que se chocou com o solo, em função de e .
Questão 21
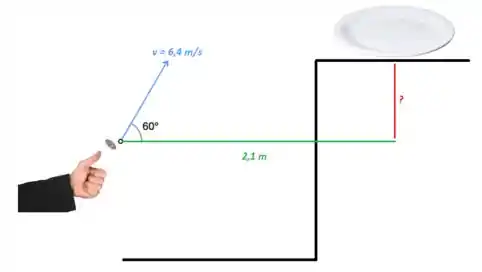
Em uma tenda de parque de diversões, você ganha uma girafa de pelúcia se você acertar uma moeda de 25 centavos em um pequeno prato. O prato está em uma prateleira acima do ponto que a moeda deixa sua mão e está a uma distância horizontal de desse ponto (imagem abaixo). Se você lançar a moeda com velocidade de com um ângulo de acima da horizontal, a moeda cai no prato.
(a)Qual é a altura da prateleira acima do ponto que a moeda abandona sua mão.
Questão 22
Um canhão localizado a da base de uma colina de de altura atira uma bala de a um ângulo de acima da horizontal na direção do penhasco.
(b) O piso no topo da montanha é plano, com uma elevação constante de acima do canhão. Nas condições da parte (a), qual a distância que o projeto percorre a partir da ponta da colina?
Ver solução completaQuestão 23
Em uma tenda de parque de diversões, você ganha uma girafa de pelúcia se você acertar uma moeda de 25 centavos em um pequeno prato. O prato está em uma prateleira acima do ponto que a moeda deixa sua mão e está a uma distância horizontal de desse ponto (imagem abaixo). Se você lançar a moeda com velocidade de com um ângulo de acima da horizontal, a moeda cai no prato.
(b) Qual é a componente vertical da velocidade da moeda no instante antes dela cair no prato.
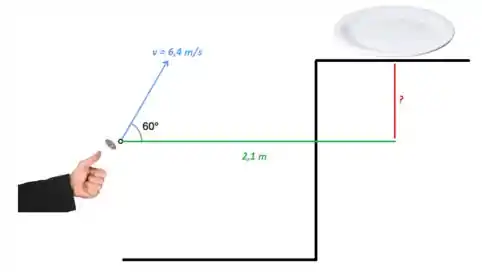
Questão 24
Um canhão localizado a da base de uma colina de de altura atira uma bala de a um ângulo de acima da horizontal na direção do penhasco.
(a) Qual deve ser a velocidade mínima que o projétil deixa o canhão para que o mesmo consiga passar pelo topo da montanha?
Ver solução completaQuestão 25
Uma arma dispara um projétil de massa com velocidade (medida em relação à arma) formando um ângulo com a horizontal. O ponto de disparo está situado a uma altura acima do solo.
a) Quais são as forças que atuam no projétil na posição de altura máxima e imediatamente antes de atingir o solo? Despreze os efeitos de resistência do ar.
b) Calcule a altura máxima do projétil, medida com relação ao solo.
c) Se em a arma é abandonada em queda livre da altura a partir do repouso. Qual é a altura máxima atingida pelo projétil, medida com relação ao solo, se o disparo acontece no tempo ?
Obs.: Dê suas respostas em função dos dados do problema e de , somente.
Ver solução completaQuestão 26
Dois canhões apontam-se mutuamente, como mostrado na figura, e disparam suas balas no mesmo instante de tempo. O canhão dispara sua bala com velocidade de módulo , e o canhão com velocidade . As distâncias no problema são .
a) Qual a aceleração de cada uma das balas após o disparo?
b) Quanto tempo se passou a partir do momento do disparo até o instante da colisão? A que altura acontece a colisão?
c) Se não houvesse o canhão , qual seria o alcance da bala do canhão A?
Ver solução completaQuestão 27
Na figura abaixo um motor exerce uma força constante para a direita sobre uma massa que cai livremente e que se encontrava inicialmente em repouso. Não há força de resistência do ar nem atrito.
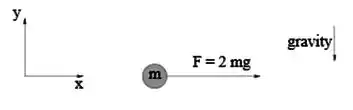
O objeto:
a) se move em linha reta com aceleração igual a .
b) se move em linha reta com aceleração igual a.
c) se move numa trajetória parabólica com aceleração igual a .
d) se move numa trajetória parabólica com aceleração igual a .
e) não é possível calcular a trajetória ou a magnitude da aceleração com os dados fornecidos pelo problema.
Ver solução completaQuestão 28
Um projétil é lançado por um canhão para atingir um alvo a uma distância , situada à mesma altura, com velocidade inicial . Um míssil balístico defensivo é lançado a partir do alvo, também a velocidade , quando o projétil atinge a sua altura máxima. Despreze a resistência do ar e considere a aceleração da gravidade como . Considere o míssil também em queda livre e tome o instante quando o míssil é lançado.
Calcule a altura máxima atingida pelo projétil.
Supondo que o ângulo de lançamento do míssil defensivo é suplementar ao de lançamento do projétil, determine esse ângulo em termos das quantidades dadas no enunciado.
Ver solução completaQuestão 29
Você tem um estilingue que arremessa projéteis a uma velocidade de , e pretende atingir alguns alvos com esse estilingue. Assuma que .
(a) Qual a distância horizontal máxima que você pode atingir com o seu projétil, assumindo que você atira o projétil desde o solo, e que o alvo também está no solo, na mesma altura do estilingue?
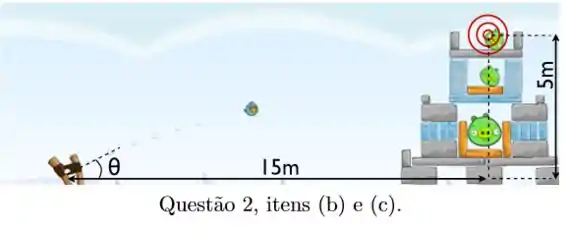
(b) Você quer arremessar o seu projétil (digamos, um “angry bird”) e atingir um alvo (digamos, um porquinho) que se encontra a uma distância de na horizontal, e a uma altura de na vertical, como indicado na Figura. Encontre a equação que determina o valor de a tangente do ângulo com o qual você deverá inclinar o seu estilingue. ( Dica: lembre-se que ).
(c) Agora, considere que entre o seu estilingue e o alvo existe um obstáculo que impede que você lance os projéteis com uma inclinação menor que 60°, ou seja, você só pode lançar projéteis com ângulos . Qual é o valor de que permite que você atinja o seu alvo?
Ver solução completaQuestão 30
Um projétil é disparado do solo, direcionado a um ângulo de 60° em relação à horizontal com velocidade inicial . No mesmo instante em que é disparado, um alvo é abandonado a de altura, estando na mira da posição inicial do projétil (vide figura). Determine:
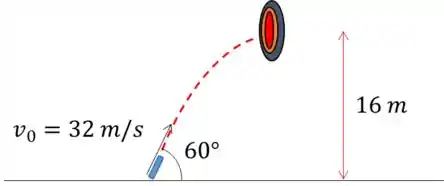
a) o vetor posição do alvo, no instante em que ele é abandonado.
b) o vetor posição e o vetor velocidade do alvo no instante em que ele é atingido pelo projétil.
c) Supondo as mesmas condições iniciais, onde apenas o módulo da velocidade inicial do projétil possa ser modificada. Qual será o intervalo possível para (onde é sempre positivo), de forma que o projétil atinja o alvo enquanto este estiver em movimento?
Ver solução completaQuestão 31
Em um projeto escolar para estudo balístico, um estudante precisa lançar uma bola de gude em uma caçapa que fica a uma distância horizontal e altura do ponto de lançamento. Ele resolve ajustar o ângulo de lançamento a .
a) Qual deve ser a velocidade inicial de lançamento?
b) Qual será a altura máxima atingida?
c) Qual será o tempo de voo da bolinha?
Ver solução completaQuestão 32
[ENUNCIADO COMUM ÀS QUESTÕES 1, 2 e 3 do 2°EE 2017.2]
Um esquiador de massa parte do repouso do ponto A, a uma altura acima da extremidade de uma rampa para saltos de esqui. Ele deixa a rampa no ponto B, fazendo um ângulo com a horizontal. O esquiador então atinge sua altura máxima no ponto C. Despreze os efeitos da resistência do ar e do atrito com a rampa. Dados: ; e .
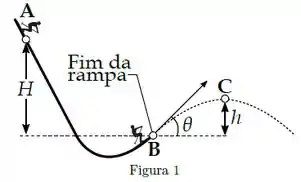
[Questão 2]
Achamos
[Questão 3 - ANULADA]
A altura máxima atingida pelo esquiador é:
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
Ver solução completaQuestão 33
Ao ser atingida por um taco, uma bola de golfe deixa o solo fazendo um ângulo
de com a horizontal a uma velocidade de . Despreze a resistência do ar.
(a) Qual a altura máxima atingida pela bola?
(b) A que distância do ponto em que foi feita a tacada a bola atinge o solo?
Ver solução completaQuestão 35
Um projétil é disparado verticalmente para cima com velocidade de módulo . Um vento imprime ao projétil uma aceleração horizontal constante de intensidade .
Determine a distância do projétil ao ponto de lançamento no instante em que ele alcança a altura máxima.
Determine o vetor velocidade do projétil no instante em que ele retorna ao nível original de lançamento.
Obtenha a equação da trajetória do projétil.
Ver solução completaQuestão 36
Um avião monomotor, à altitude de , deixa cair uma caixa. No instante em que a caixa é largada, o avião voava a inclinado de acima da horizontal. Despreze a resistência do ar.
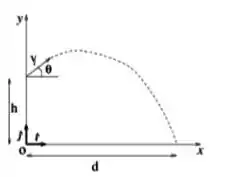
- A caixa atinge o solo a que distância horizontal do ponto em que é largada;
- Qual é o vetor velocidade da caixa ao se chocar com o solo.
Questão 40
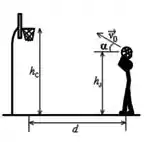
Na figura abaixo, o jogador precisa lançar a bola com um vetor velocidade inicial correto (isto é, módulo, direção e sentido corretos) para conseguir acertar a cesta. O vetor possui módulo e forma um ângulo com a direção horizontal. O jogador está a uma distância horizontal da cesta, lança a bola de uma altura , e a cesta está a uma altura . Despreze a resistência do ar e efeitos devido à rotação da bola. Considere , .
a) Encontre uma expressão para o valor do módulo de modo que a bola atinja a cesta.
b) Se , escreva os vetores velocidade e aceleração da bola no instante em que ela atinge a cesta.
c) Se pudermos variar o ângulo e a velocidade inicial, determine geometricamente qual o critério adicional devemos considerar para que a bola entre na cesta, considerando que além de alcançá-la a bola deverá necessariamente estar na descendente.
Questão 41
Dois projéteis são lançados ao mesmo tempo. O primeiro com velocidade inicial de módulo e inclinação com relação à horizontal e o segundo com velocidade inicial de módulo e inclinação com relação à horizontal. Despreze a resistência do ar. Se , e qual das afirmativas abaixo é verdadeira?
Escolha uma:
As alturas máximas atingidas pelos dois projéteis são as mesmas e ocorrem no mesmo instante .
As alturas máximas atingidas pelos dois projéteis são as mesmas e ocorrem nos instantes e , onde .
A altura máxima atingida pelo projétil é maior que a do projétil e ocorrem no mesmo instante .
A altura máxima do projétil é maior que a do projétil e ocorrem nos instantes e , onde
A altura máxima atingida pelo projétil é menor que a do projétil e ocorrem no mesmo instante .
A altura máxima do projétil é menor que a do projétil e ocorrem nos instantes e , onde
Não há dados suficientes para responder à pergunta.
Nenhuma das alternativas é verdadeira
Ver solução completaQuestão 42
Um projétil é lançado próximo à superfície da Terra, fazendo um ângulo com a horizontal. No momento do lançamento uma corrente de ar está presente e produz uma força horizontal de módulo constante e não nulo agindo da esquerda para a direita. A trajetória do projétil sob a ação das forças peso é mostrada na figura. Considerando o ponto A da trajetória, os vetores que representam a aceleração e a velocidade do projétil, respectivamente, são os indicados pelos números
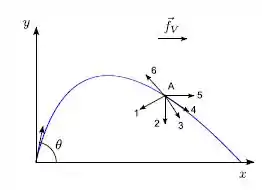
- 3 e 4
- 2 e 4
- 1 e 4
- 2 e 5
- 6 e 4
Questão 43
Uma pedra é arremessada do alto de um prédio de altura em relação ao solo, com velocidade de módulo e que faz um ângulo em relação à horizontal, com componente vertical inicial positiva. É correto afirmar que:
(a) A aceleração sobre a pedra é constante durante o movimento.
(b) A pedra atingirá o solo com velocidade de módulo .
(c) A pedra atinge o solo um tempo após ter sido lançada.
(d) O tempo que a pedra leva para atingir a altura máxima é o mesmo que ela leva para ir da altura máxima ao solo.
(e) No ponto de altura máxima a pedra tem velocidade nula.
(f) No ponto de altura máxima a pedra tem aceleração nula.
Ver solução completaQuestão 45
(Cap 3 – Ex 76) Um projétil é lançado do nível do chão com uma rapidez inicial de 53 m/s. Encontre o ângulo de lançamento (o ângulo que o vetor velocidade inicial forma acima da horizontal) de forma que a altura máxima do projétil seja igual ao seu alcance horizontal. (ignore a resistência do ar.)
Ver solução completaQuestão 46
PARTE I
No instante , uma partícula possui velocidade em relação ao solo, onde e (ver figura). Ela se move sob ação da aceleração da gravidade no eixo . Sabe-se que em ela alcança a altura máxima e que nesse instante, no referencial de um observador que possui velocidade , a velocidade da partícula é no sentido do eixo positivo.
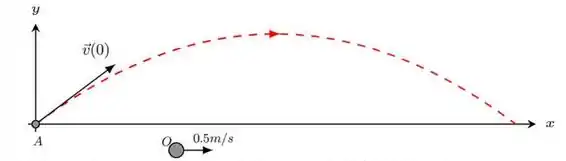
- Determine, em termos dos vetores unitários, o vetor velocidade inicial da partícula .
Questão 47
Três projéteis A, B e C são lançados da mesma posição inicial do solo com velocidades iniciais de mesmo módulo e que fazem três ângulos diferentes , e , respectivamente com a direção horizontal. Sabendo-se que e que o que pode-se afirmar sobre os tempos que cada projétil leva para atingir novamente o solo?
(a)
(b)
(c)
(d)
(e) Não é possível relacionar os tempos sem saber o módulo da velocidade inicial.
Ver solução completaQuestão 48
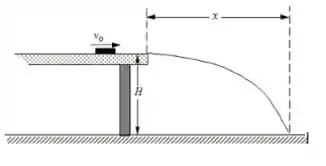
Um pequeno disco desliza com rapidez sobre uma mesa horizontal lisa de altura . Após abandonar a mesa, o disco atinge o chão num ponto à distância horizontal da borda da mesa, como mostrado na figura. É correto afirmar que a relação entre e é ?
(A)
(B)
(C)
Ver solução completaQuestão 49
Preencha cada campo com sua resposta.
Uma partícula é lançada com velocidade inicial , onde e são os vetores unitários usuais ao longo dos eixos (horizontal) e (vertical, orientado para cima), respectivamente.
Considere e despreze quaisquer efeitos de resistência do ar.
- Quanto tempo depois do lançamento a partícula atinge a altura máxima?
- Decorridos após o lançamento, qual é o vetor velocidade da partícula (em termos dos vetores unitários)? .
Questão 50
. Um canhão dispara um projétil da forma mostrada na figura. A reta tracejada mostra a trajetória do projétil na ausência de gravidade; os pontos correspondem às posições do projétil a intervalos de um segundo. Se , as distâncias são:
Ver solução completaQuestão 51
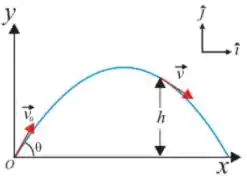
Q. Uma bola é lançada para o alto a partir da origem de um sistema cartesiano . A magnitude do vetor velocidade inicial é e o ângulo de lançamento é . Quando a bola atinge a altura , como na figura, o vetor velocidade da bola é , com unidades no . Considerando a resistência do ar desprezível, a distância horizontal no primeiro choque da bola com o solo, a partir da origem, medida em metros, é:
Questão 53
(Cap 3 – Ex 106) Consertando o telhado de sua casa, você deixa o martelo cair acidentalmente. O martelo escorrega pelo telhado a uma rapidez constante de 4,0 m/s. O telhado faz ângulo de 30° com a horizontal e seu ponto mais baixo está 10 m acima do chão. (a) Em quanto tempo, após abandonar o telhado, o martelo chega ao chão? (b) Qual é a distância horizontal percorrida pelo martelo, entre o instante em que abandona o telhado e o instante em que se choca com o chão? (Ignore a resistência do ar.)
Ver solução completaQuestão 54
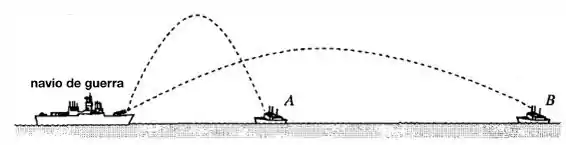
Um navio de guerra atira simultaneamente dois mísseis em navios inimigos. Se os mísseis seguem as trajetórias parabólicas mostradas, qual das afirmações é correta:
(a) Só é possível determinar a ordem de chegada dos mísseis conhecendo-se o valor exato dos ângulos de lançamento.
(b) O navio B é atingido primeiro.
(c) Só é possível determinar a ordem de chegada dos mísseis conhecendo-se as magnitudes das velocidades de lançamento.
(d) O navio A é atingido primeiro.
(e) Os navios A e B são atingidos simultaneamente.
Ver solução completaQuestão 55
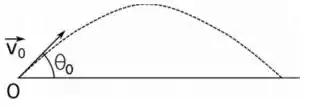
4 – Um projétil de massa é lançado com um ângulo com a horizontal, como mostra a figura, com velocidade inicial .
a) calcule o módulo do torque realizado pela gravidade sobre a bola de canhão, em relação ao ponto de lançamento , em .
b) Qual a direção e sentido do torque nesse instante?
c) Calcule o momento angular da bala de canhão em relação ao ponto , nesse mesmo instante.
d) Qual a direção e sentido do momento angular nesse instante?
Ver solução completaQuestão 56
Um projétil é lançado a partir da posição inicial , no solo, com velocidade escalar inicial . O instante inicial é tomado como , o solo em toda a região é horizontal e coincide com o eixo , e a aceleração da gravidade é dada por . O projétil toca novamente o solo em . Considere os eixos como horizontal e vertical respectivamente.
a) Dado que o ângulo de lançamento com a horizontal foi , encontre a equação da trajetória descrita pelo projétil durante seu movimento até atingir o solo.
b) Encontre o tempo que o projétil leva para atingir o solo. Encontre também o ângulo que o vetor velocidade faz com a horizontal ao atingir o solo.
c) No ponto mais alto da trajetória, o vetor velocidade do projétil faz um ângulo de com a horizontal. Calcule, para este instante, o raio de curvatura da trajetória. (Dica: pense na aceleração centrípeta, que é a componente da aceleração perpendicular à velocidade.)
Ver solução completaQuestão 57
Um canhão, posicionado sobre um terreno completamente plano, dispara um projétil com um velocidade inicial de módulo fazendo um ângulo de com a horizontal. Considerando a posição incial do canhão como origem do sistema de coordenadas e a aceleração da gravidade determine:
O tempo total de voo do projétil.
O vetor posição do projétil quando o mesmo atinge sua altura máxima.
O vetor velocidade quando o mesmo atinge o solo.
Considere agora que o projétil deva atingir um alvo que está a uma distância de do canhão. Qual deve ser o ângulo de tiro para que o projétil com velocidade inicial de módulo possa atingir o alvo?
Ver solução completaQuestão 58
Em um lançamento de projétil com um ângulo em relação a vertical não nulo, é correto afirmar que os vetores velocidade e aceleração:
a) São perpendiculares no ponto mais alto da trajetória;
b) São paralelos somente nos pontos de lançamento e logo antes do projétil atingir o solo
c) São sempre paralelos, durante toda a trajetória;
d) Têm módulos proporcionais;
e) Ambos apresentam um valor máximo no ponto mais alto da trajetória.
Ver solução completaQuestão 59
Num jogo de futebol, um jogador chuta a bola em direção ao gol com uma velocidade inicial que faz um ângulo com a direção horizontal. Despreze a resistência do ar e trate a bola como um objeto pontual. Suponha que o gol esteja a uma distância horizontal do ponto do chute, e possua altura, conforme figura abaixo.
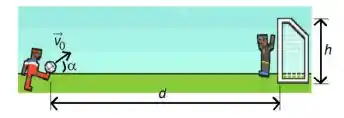
b) Quanto tempo a bola leva nesse percurso (entre o chute e a colisão com a trave superior)?
Ver solução completaQuestão 60
Num jogo de futebol, um jogador chuta a bola em direção ao gol com uma velocidade inicial que faz um ângulo com a direção horizontal. Despreze a resistência do ar e trate a bola como um objeto pontual. Suponha que o gol esteja a uma distância horizontal do ponto do chute, e possua altura, conforme figura abaixo.
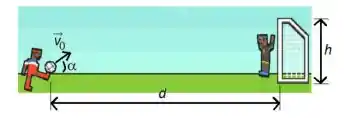
a) Qual deve ser a velocidade inicial para que a bola bata na trave superior (travessão) do gol?
Ver solução completaQuestão 61
Num jogo de futebol, um jogador chuta a bola em direção ao gol com uma velocidade inicial que faz um ângulo com a direção horizontal. Despreze a resistência do ar e trate a bola como um objeto pontual. Suponha que o gol esteja a uma distância horizontal do ponto do chute, e possua altura, conforme figura abaixo.
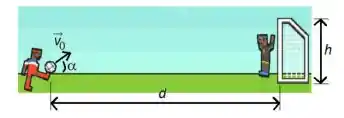
c) Com que ângulo a bola atinge a trave superior? Ela atinge a trave superior durante sua subida ou descida? Justifique.
Ver solução completaQuestão 62
Num jogo de futebol, um jogador chuta a bola em direção ao gol com uma velocidade inicial que faz um ângulo com a direção horizontal. Despreze a resistência do ar e trate a bola como um objeto pontual. Suponha que o gol esteja a uma distância horizontal do ponto do chute, e possua altura, conforme figura abaixo.
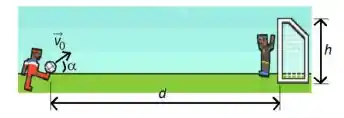
d) Considerando o mesmo valor de encontrado no item (a), escreva uma equação que permita encontrar outro valor de que também faz a bola acertar o travessão (não precisa resolver a equação).
Ver solução completaQuestão 63
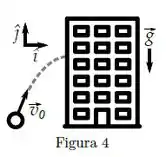
Uma partícula é lançada do solo no instante com velocidade (em ) (ver Figura 4). No instante , a partícula se choca com um edifício. Qual é a altura (em relação ao solo) do ponto de colisão? Use .
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
Ver solução completaQuestão 64
(inspirada no 2° testinho) Uma partícula é lançada do solo com velocidade de módulo , fazendo um ângulo com a horizontal, tal que e . Após , a partícula colide com o ponto A da figura abaixo. Despreze a resistência do ar e
considere .
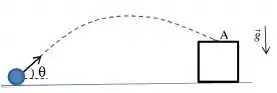
(a) Qual é a altura do ponto A em relação ao ponto de partida?
(b) Determine o vetor velocidade da partícula imediatamente antes da colisão com o ponto
A.
Ver solução completaQuestão 65
Uma bola é chutada e percorre uma trajetória parabólica antes de atingir o chão. Qual das seguintes afirmações é verdadeira?
A) A aceleração da bola diminui à medida que ela sobe.
B) A velocidade da bola é zero quando ela atinge o ponto mais alto da trajetória.
C) A aceleração da bola é zero quando ela atinge o ponto mais alto da trajetória.
D) O módulo da velocidade da bola é mínimo quando ela atinge o ponto mais alto da trajetória
E) O módulo da velocidade da bola é máximo quando ela atinge o ponto mais alto da trajetória.
Ver solução completaQuestão 66
Uma bola de neve de é lançada de um penhasco de de altura. A velocidade inicial da bola de neve é de , acima da horizontal. Qual é o trabalho realizado sobre a bola de neve pela força gravitacional durante o percurso até um terreno plano, abaixo do penhasco? Qual é a variação da energia potencial do sistema bola-de-neve Terra durante o percurso? Se a energia potencial gravitacional é tomada como sendo nula na altura do penhasco, qual é o seu valor quando a bola de neve chega ao solo?
Ver solução completaQuestão 67
João e Pedro estão no topo de um prédio. Eles jogam uma bola cada, ao mesmo tempo. João arremessa sua bola verticalmente para baixo. Pedro arremessa sua bola para frente e para baixo, fazendo um ângulo de com a horizontal. A rapidez inicial da bola de Pedro é o dobro da de João. Supondo que não haja desníveis no chão próximo ao prédio, qual das bolas atinge o solo primeiro?
(A) A bola de Pedro.
(B) A bola de João.
(C) Elas chegam ao solo ao mesmo tempo.
(D) A resposta depende da altura do prédio.
(E) A resposta depende do módulo das velocidades iniciais.
Ver solução completaQuestão 68
Um objeto é lançado com velocidade inicial como ilustrado na figura abaixo. Qual das alternativas melhor representa a direção da aceleração no ponto A.
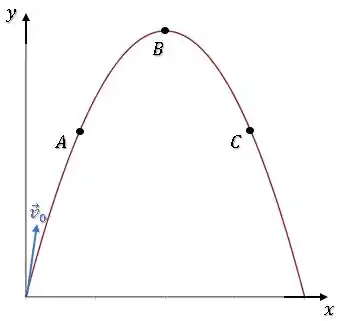
Figura: Trajetória de um objeto lançado próximo à superfície com uma velocidade
Questão 69
Tiroteio deixa três vítimas de bala perdida no Subúrbio do Rio
As Vítimas estavam em um bar em Oswaldo Cruz, um bairro do Subúrbio.
Do G1 Rio
Três pessoas foram vítimas de balas perdidas em um bar na Rua Engenheiro Antonio Rieldlinger, em Oswaldo Cruz, no Subúrbio do Rio, na madrugada deste domingo (24).
De acordo com informações do 9º BPM (Rocha Miranda), Adilson das Neves da Cruz Junior, de 15 anos, Bruno Pinada Hora, de 25 anos e Flávia Regina Alves, de 36 anos, estavam no estabelecimento comercial, quando dois homens passaram próximo ao local trocando tiros.
Adaptado
A reportagem mostra mais uma cena de violência das grandes cidades, esta ocorreu no Rio de Janeiro.
Uma das balas perdidas foi projetada da arma com um ângulo cujo vale e o vale 0,8 e a velocidade inicial de .
Sabendo-se que a aceleração gravitacional vale , podemos afirmar que o tempo de subida do projétil, em , vale:
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 70
PARTIDA DE FUTEBOL
"A chuteira veste o pé descalço
O tapete da realeza é verde
Olhando para bola eu vejo o sol
Está rolando agora, é uma partida de futebol
O meio campo é lugar dos craques
Que vão levando o time todo pro ataque
O centroavante, o mais importante
Que emocionante, é uma partida de futebol"
Trecho da canção Partida de Futebol, interpretada pelo grupo Skank e composta por Nando Reis e Samuel Rosa.
Um centroavante chuta a bola em certa direção com velocidade inicial , A trajetória descrita é parabólica e o projétil toca o solo horizontal em . Desprezando a resistência do ar, podemos afirmar que a opção FALSA, é:
(a) O tempo que a bola leva para subir e descer é igual ao tempo dela atingir o seu alcance máximo.
(b) o chute atinge a velocidade zero no eixo y no ponto mais alto da trajetória.
(c) A aceleração vetorial no eixo x é constante.
(d) O movimento do eixo y possui a aceleração da gravidade.
(e) O movimento do eixo x é um MUV e do eixo y é MU
Ver solução completaQuestão 71
Em 24/02/2013 07h54 - Atualizado em 24/02/2013 08h29.
Tiroteio deixa três vítimas de bala perdida no Subúrbio do Rio
As Vítimas estavam em um bar em Oswaldo Cruz, um bairro do Subúrbio.
Do G1 Rio
Três pessoas foram vítimas de balas perdidas em um bar na Rua Engenheiro Antonio Rieldlinger, em Oswaldo Cruz, no Subúrbio do Rio, na madrugada deste domingo (24).
De acordo com informações do 9º BPM (Rocha Miranda), Adilson das Neves da Cruz Junior, de 15 anos, Bruno Pinada Hora, de 25 anos e Flávia Regina Alves, de 36 anos, estavam no estabelecimento comercial, quando dois homens passaram próximo ao local trocando tiros.
Adaptado
A reportagem mostra mais uma cena de violência das grandes cidades, esta ocorreu no Rio de Janeiro.
Uma das balas perdidas foi projetada da arma com um ângulo cujo vale e o vale 0,8 e a velocidade inicial de .
Sabendo-se que a aceleração gravitacional vale , podemos afirmar que o tempo de subida do projétil, em , vale:
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 72
Suponha que uma rã possa pular sempre com a mesma velocidade inicial em qualquer direção que ela pule (ela pode pular para frente ou diretamente de baixo para cima). Como a altura máxima () que ela pode atingir se relaciona com o alcance horizontal máximo ?
(a)
(b)
(c)
(d)
(e)
(f) Não há como saber sem conhecer o valor de .
Ver solução completaQuestão 73
Suponha que em uma partida de futebol, o goleiro, ao bater o tiro de meta, chuta a bola, imprimindo-lhe uma velocidade cujo vetor forma, com a horizontal, um ângulo. Desprezando a resistência do ar, são feitas as seguintes afirmações.
I – No ponto mais alto da trajetória, a velocidade vetorial da bola é nula.
II – A velocidade inicial pode ser decomposta segundo as direções horizontal e vertical.
III – Se a bola alcançará a maior distância horizontal possível.
IV – No ponto mais alto da trajetória o valor da componente vertical da velocidade é nulo.
Estão corretas:
A) I, II e III
B) II, III e IV
C) II e IV
D) III e IV
E) I e II
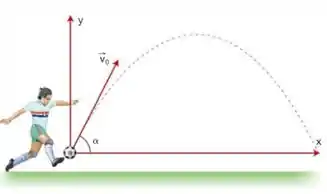
Questão 74
Um projétil é lançado a partir do solo com vetor velocidade inicial de módulo 10 m/s, fazendo um ângulo com o eixo x horizontal. Sabe-se que cos = 0,80 e sen = 0,60. Considere . Despreze a resistência do ar.
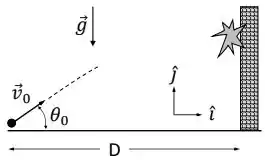
Após percorrer uma distância horizontal D = 8,0 m, o projétil se choca com um muro. Imediatamente antes deste choque, o vetor velocidade do projétil é, em m/s:
a)
b
c)
d)
e)
f)
g)
h)
i)
Ver solução completaQuestão 75
Um navio de guerra tenta bombardear simultaneamente dois navios A e B. Se os projéteis são disparados com velocidades cujas magnitudes são idênticas e seguem as trajetórias mostradas na figura abaixo, qual dos navios é atingido primeiramente? Despreze a resistência do ar
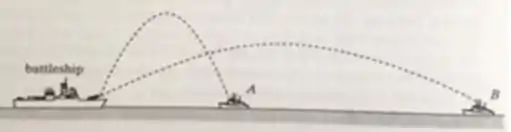
- A.
- B.
- Os dois são atingidos simultaneamente.
- Mais informação é necessária para se responder esta questão.
- Nenhuma das alternativas é correta
Questão 76
[Enunciado comum às Questões 1 e 2]
Uma bola é lançada com velocidade acima da horizontal e leva para atingir a parede.
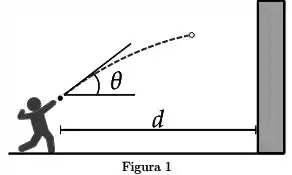
[Questão 2]
Ao atingir a parede, o deslocamento vertical da bola é:
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
(i)
Ver solução completaQuestão 77
Um pedreiro tem que lançar um tijolo para um colega localizado no segundo andar de um prédio em construção. O pedreiro que lança o tijolo encontra-se no solo a 1 metro do prédio, e seu colega encontra-se a 2 metros de altura em relação ao ponto de lançamento. A velocidade impressa ao projétil é tal que este atinge o segundo andar no ponto de maior altura de sua trajetória. A que ângulo com a horizontal o projétil foi lançado?
a) 30°
b) 45°
c) 60°
d)
e)
Ver solução completaQuestão 78
4 - No movimento usual de um projétil, quando o projétil está no ponto mais alto de sua trajetória, podemos afirmar que:
A) Sua aceleração é zero.
B) Sua velocidade é perpendicular à sua aceleração.
C) Sua velocidade e sua aceleração são iguais à zero.
D) A componente horizontal da sua velocidade é zero.
E) A componente vertical e a componente horizontal de sua velocidade são iguais à zero.
Ver solução completaQuestão 79
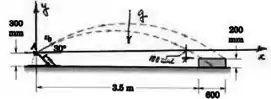
Uma equipe de estudantes de engenharia está projetando uma catapulta para lançar uma pequena bola em A de modo que ela caia na caixa. Sabendo que o vetor velocidade inicial faz um ângulo de com a horizontal.
- Obtenha a equação da trajetória
- Determine a faixa de velocidades de lançamento com a qual a bola cairá dentro da caixa
Questão 80
Questão 1) Um participante de desafios pretende chutar uma bola, inicialmente parada no chão de uma quadra, para acertar uma cesta de basquete, a uma altura do chão. Seja o módulo da velocidade imprimida à bola pelo chute, o ângulo entre o vetor velocidade inicial e a quadra e o módulo da aceleração gravitacional, determine:
a) O tempo decorrido entre o chute e o instante que a bola atinge a cesta (aro).
b) O vetor velocidade ao atingir o aro.
c) Com base nos seus resultados, a bola ao atingir o aro já passou pelo ponto mais alto da trajetória? Justifique sua resposta.
Ver solução completaQuestão 81
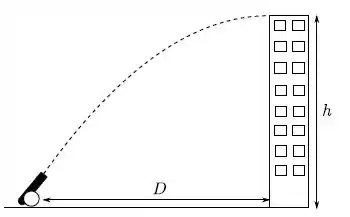
Um canhão encontra-se a uma distância horizontal de uma torre cujo topo está a uma altura . Para que uma bala disparada pelo canhão atinja o topo da torre horizontalmente, como mostra a figura, a tangente do ângulo de disparo deve ser:
Questão 83
Considere que um míssil de massa e velocidade inicial é lançado do solo fazendo um ângulo de como mesmo. Suponha que o míssil, ao alcançar sua altura máxima, se divide em duas partes: uma de massa e outra de massa , sendo que a parte com a massa menor cai verticalmente para baixo. Desprezando-se a resistência do ar e supondo que as duas partes tocam o solo ao mesmo tempo, calcule:
- a posição em que o centro de massa das duas massas toca o solo.
- a posição em que a parte com a massa maior toca o solo.
Questão 84
Um canhão antitanque está localizado na borda de um platô a acima de uma planície, conforme a figura abaixo. A equipe do canhão avista um tanque inimigo parado na planície à distância de do canhão. No mesmo instante, a equipe do tanque avista o canhão e começa a se mover em linha reta para longe deste. com aceleração de . O canhão antitanque dispara um projétil com velocidade de disparo de e com ângulo de acima da horizontal.

Quanto tempo a equipe do canhão teria de esperar antes de atirar, se quiser acertar o tanque?
Com que ângulo o projétil atinge o tanque?
Ver solução completaQuestão 85
Uma bola, de dimensões reduzidas, é lançada do nível do solo com uma certa velocidade inicial de módulo conhecido, atinge o solo novamente a uma certa distância do ponto de lançamento. Dependendo do ângulo de lançamento que o vetor velocidade inicial faz com a direção horizontal, essa distância varia. A figura abaixo dá o alcance da bola para uma mesma velocidade inicial quando variamos o ângulo de lançamento.
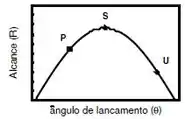
O módulo da velocidade ao alcançar a altura máxima, para cada um dos três ângulos de lançamento indicados na figura, obedece a relação:
(a)
(b)
(c)
(d)
(e)
(f)
Ver solução completaQuestão 87
A maior parte deste problema se refere a seção do livro do Taylor
a) Encontre a velocidade e a posição de uma esfera de massa submetida a gravidade e a uma força de arrasto proporcional ao quadrado da velocidade:
Particularmente, para objetos esféricos, pode ser reescrito como:
sendo o diâmetro e depende do meio. O valor de para objetos esféricos no ar
Calcule a velocidade terminal de uma esfera em queda livre de densidade e raio .
Ver solução completaQuestão 88
O movimento de uma partícula que se move em uma dimensão é representado por uma parábola no gráfico posição x tempo, como mostrado na figura. Nos gráficos das figuras [1], [2] , [3],[4] e [5] estão representadas simultaneamente, velocidade e aceleração A velocidade está representada por uma linha contínua enquanto que a aceleração por uma linha tracejada. O gráfico que representa corretamente descreve a velocidade e aceleração da partícula em questão é
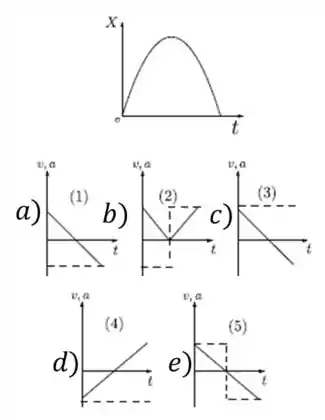
Questão 89
(Cap 3 – Ex 75) Na Figura 3-35, qual é a rapidez inicial mínima que o dardo deve ter para atingir o macaco antes que este chegue ao chão, que está abaixo da posição inicial do macaco, se e ? (Ignore a resistência do ar.)
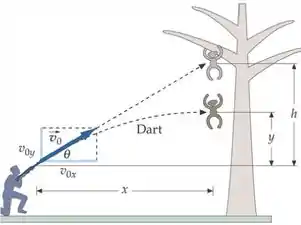
Questão 90
(Cap 4 – Ex 47) Um rebatedor golpeia uma bola de beisebol quando o centro da bola está acima do solo. A bola deixa o taco fazendo um ângulo de com o solo e com uma velocidade tal que o alcance horizontal (distância até voltar à altura de lançamento) é .
(a) A bola consegue passar por um alambrado de de altura que está a uma distância horizontal de do ponto inicial?
(b) Qual é a distância entre a extremidade superior do alambrado e o centro da bola quando a bola chega ao alambrado?
Ver solução completaQuestão 91
(Cap 4 – Ex 28) Uma pedra é lançada por uma catapulta no instante , com uma velocidade inicial de módulo e ângulo acima da horizontal. Quais são os módulos das componentes
(a) horizontal e (b) vertical do deslocamento da pedra em relação à catapulta em ? Repita os cálculos para as componentes (c) horizontal e (d) vertical em s
e para as componentes (e) horizontal e (f) vertical em .
Ver solução completaQuestão 92
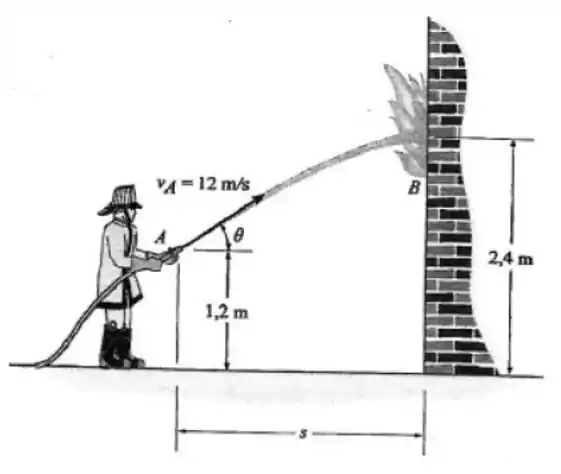
Uma mangueira, com o bico localizado 1, 5 m acima do solo, é apontada para cima, segundo um ângulo de 30◦ com o chão. O jato de água atinge um canteiro a 15 m de distância.
b. Que altura ele atinge??
Ver solução completaQuestão 93
(Cap 4 – Ex 38) Você lança uma bola em direção a uma parede com uma velocidade de e um ângulo acima da horizontal (Fig. 4-38). A parede está a uma distância do ponto de lançamento da bola.
(a) A que distância acima do ponto de lançamento a bola atinge a parede?
Quais são as componentes (b) horizontal e (c) vertical da velocidade da bola ao atingir a parede?
(d) Ao atingir a parede, a bola já passou pelo ponto mais alto da trajetória?
Ver solução completaQuestão 94
(Capítulo 4.6 – Ex.54) Dois segundos após ter sido lançado a partir do solo, um projétil deslocou-se horizontalmente e verticalmente em relação ao ponto de lançamento. Quais são as componentes (a) horizontal e (b) vertical da velocidade inicial do projétil? (c) Qual é o deslocamento horizontal em relação ao ponto de lançamento no instante em que o projétil atinge a altura máxima em relação ao solo?
Ver solução completaQuestão 95
Um avião bombardeiro, a de altitude, voa em perseguição a um carro, no solo, que viaja a . Em dado instante, o avião lança uma bomba com velocidade escalar igual a , fazendo um ângulo de 30◦ com a horizontal. A que distância horizontal do carro deve ser lançada a bomba para que acerte o alvo?
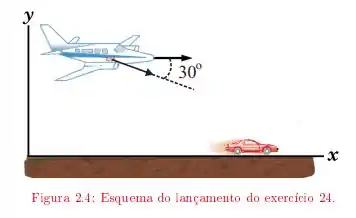
Questão 96
(Capítulo 4.6 – Ex.55) Na Fig. 4-48, uma bola de beisebol é golpeada a uma altura e apanhada na mesma altura. Deslocando-se paralelamente a um muro, passa pelo alto do muro após ter sido golpeada e, novamente, depois, quando está descendo, em posições separadas por uma distância . (a) Qual é a distância horizontal percorrida pela bola do instante em que foi golpeada até ser apanhada? Quais são (b) o módulo e (c) o ângulo (em relação à horizontal) da velocidade da bola imediatamente após ter sido golpeada? (d) Qual é a altura do muro?
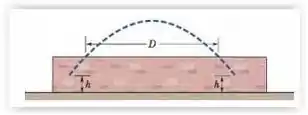
Questão 98
(Cap 4 – Ex 37) Uma bola é lançada a partir do solo. Quando atinge uma altura de , a velocidade é , com horizontal e para cima.
(a) Qual é a altura máxima atingida pela bola?
(b) Qual é a distância horizontal coberta pela bola?
Quais são (c) o módulo e (d) o ângulo (abaixo da horizontal) da velocidade da bola no instante em que atinge o solo?
Ver solução completaQuestão 99
No lançamento oblíquo, podemos afirmar que o movimento resultante tem uma trajetória que é uma composição de movimentos nos eixos horizontal e vertical, respectivamente. Esses movimentos são classificados como:
(a) movimento uniforme e movimento uniformemente variado.
(b) movimento uniformemente variado e movimento uniformement.e variável.
(c) movimento uniforme e movimento uniforme.
(d) movimento uniforme e movimento curcular.
(e) movimento uniformemente variado e movimento uniforme
Ver solução completaQuestão 100
Qual das linhas no gráfico abaixo melhor representa a componente vertical da velocidade vy em função do tempo t para um projétil disparado fazendo um ângulo de 45 com a horizontal?
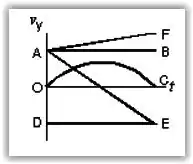
A) OC
B) DE
C) AB
D) AE
E) AF
Ver solução completaQuestão 101
Uma mangueira, com o bico localizado 1, 5 m acima do solo, é apontada para cima, segundo um ângulo de 30◦ com o chão. O jato de água atinge um canteiro a 15 m de distância.
a. Com que velocidade o jato sai da mangueira?
Ver solução completaQuestão 102
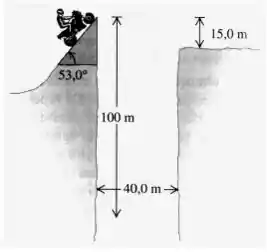
Um professor de física faz proezas loucas em suas horas vagas. Sua última façanha foi saltar sobre um
rio com sua motocicleta. A rampa de decolagem era inclinada de 53,0o, a largura do rio era de 40,0 m, e a outra margem estava a 15,0 m abaixo do nível da rampa. O rio estava a 100 m abaixo do nível da rampa. Despreze a resistência do ar.
(a) Qual deveria ser sua velocidade para que ele pudesse alcançar a outra margem sem cair no rio?
(b) Caso sua velocidade fosse igual a metade do valor encontrado em (a), onde ele cairia?
Questão 103
Um cineasta filma a erupção de um vulcão e, num certo instante, ele registra um bloco sendo arremessado fazendo um ângulo com a horizontal, partindo da boca do vulcão de uma altura a partir do solo. Ele acompanha o movimento do bloco e o filma batendo no solo, como na figura, um tempo após ser lançado. Desprezando a resistência do ar,
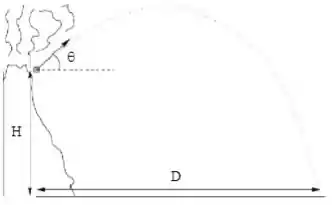
- Calcule o módulo da velocidade do bloco quando ele foi arremessado da boca do vulcão e começou a ser filmado, , em função de e .
Questão 104
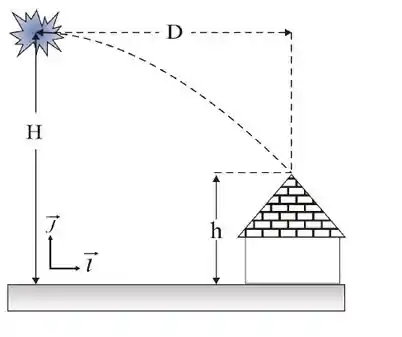
Um balão de São João, partindo do repouso, é empurrado pelo vento e desloca-se horizontalmente a uma altura do solo. Devido ao vento, a aceleração do balão é Após do início deste movimento, o balão incendeia-se instantaneamente. A tocha, sobre a qual o efeito do vento é desprezível, cai e acaba atingindo uma casa. A altura da casa é e se encontra a uma distância horizontal, a contar do ponto em que o balão incendiou-se, como mostrado na figura. Pergunta-se: qual é o vetor velocidade da tocha quando ela atinge o telhado? Dê suas respostas na base de vetores (, )
Despreze a resistência do ar.
Questão 105
Em um lançamento oblíquo sem resistência do ar, é correto afirmar que:
- A aceleração no topo da trajetória é zero.
- O movimento horizontal do projétil é uniformemente acelerado.
- O projétil tem aceleração constante no eixo vertical.
- A velocidade total na altura máxima é zero.
- O alcance máximo do lançamento se dá com um ângulo diferente de 45 graus.
Questão 106
4) Uma pessoa que se encontra em uma região plana lança um objeto para cima ao longo de uma direção que faz um ângulo com a horizontal e, simultaneamente ao lançamento, corre com aceleração de módulo ao longo da linha que contêm a projeção horizontal da posição do objeto, no sentido de recuperá-lo de volta ao cair. Para que isso aconteça a relação entre o módulo da aceleração da pessoa e o da gravidade deve ser:
a)
b)
c)
d)
e)
Ver solução completaQuestão 107
[Enunciado comum às Questões 1 e 2]
Uma bola é lançada com velocidade acima da horizontal e leva para atingir a parede.
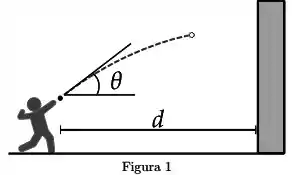
[Questão 1]
Considere as seguintes assertivas:
. A distância da parede ao ponto de lançamento é de
. A trajetória da bola é uma parábola.
. A bola atinge a parede após atingir o ponto mais alto da sua trajetória
É correto apenas o que se afirma em: ́
(a)
(b)
(c)
(d) e
(e) e
(f) e
(g) Todas
(h) Nenhuma
Ver solução completaQuestão 108
Vemos na figura duas trajetória distintas, descrevendo o movimento de dois projéteis lançados a partir do mesmo ponto, atingindo a mesma altura. Se avaliarmos a relação entre os tempos de voo, desprezando o efeito da resistência do ar, podemos dizer que:
(a) .
(b) .
(c)
(d)
(e) faltam dados para avaliar a relação entre os tempos de voo.
Ver solução completaQuestão 109
Um jogador de futebol quer lançar a bola para ele mesmo, de forma que ela encubra os adversários e ele a recupere mais à frente. Considerando que a altura máxima do lançamento é de , e a velocidade máxima do jogador é de , que distância ele vai percorrer até recuperar a bola?

(a)
(b)
(c)
(d)
(e)
Dados:
Ver solução completaQuestão 110
Um projétil está descrevendo uma trajetória parabólica e repentinamente explode. Nesta situação, é correto dizer que:
- O centro de massa do projétil descreve uma trajetória parabólica desde o lançamento apenas até o momento em que o projétil explode.
- A explosão conserva momento linear.
- O centro de massa do projétil descreve uma trajetória parabólica desde o lançamento até o momento em que o primeiro estilhaço toca o solo.
- O centro de massa do projétil descreve uma trajetória parabólica desde o lançamento até o momento em que o ultimo estilhaço toca o solo.
- I e III
- II e IV
- II e III
- III e IV
- I e II
Questão 111
Um canhão lança suas balas com uma certa inclinação em relação à horizontal. Assuma que a bala atinge o chão na mesma elevação em que foi lançada.
Se o tempo de voo foi de segundos, e o alcance da bala de canhão é de metros, qual a componente horizontal de sua velocidade?
a) 35
b)
c)
d)
e) nenhuma das anteriores.
Ver solução completaQuestão 112
![]()
Um piloto de avião deixa cair um pacote enquanto o avião voa horizontalmente com velocidade constante. Desprezando a resistência do ar, quando o pacote atinge o solo a posição horizontal do avião será
- Atrás do pacote.
- Sobre o pacote.
- Em frente ao pacote
- Depende da rapidez do avião quando o pacote é liberado
Questão 113
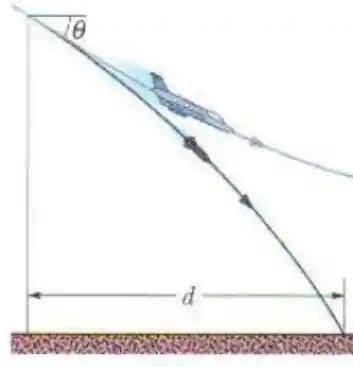
Um avião mergulhando com velocidade constante num ângulo de com a vertical libera um projétil a uma altitude de . O projétil bate no chão após ter sido liberado.
b) Que distância o projétil percorre horizontalmente durante o seu vôo?
Ver solução completaQuestão 114
Um avião mergulhando com velocidade constante num ângulo de com a vertical libera um projétil a uma altitude de . O projétil bate no chão após ter sido liberado.
c) Quais são as componentes horizontal e vertical de sua velocidade imediatamente antes de chegar ao solo?
Ver solução completaQuestão 115
Um avião mergulhando com velocidade constante num ângulo de com a vertical libera um projétil a uma altitude de . O projétil bate no chão após ter sido liberado.
a) Qual a velocidade do avião?
Ver solução completaQuestão 116
Você está a de uma parede da casa vista na figura ao lado. Você quer jogar uma bola para seu amigo que está a da parede oposta. O arremesso e a recepção ocorrem a acima do solo.
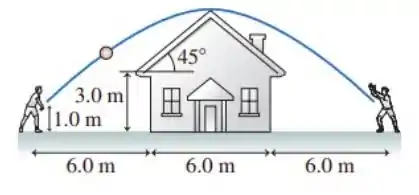
- Que velocidade mínima permitirá que a bola ultrapasse o teto?
Questão 117
Você está a de uma parede da casa vista na figura ao lado. Você quer jogar uma bola para seu amigo que está a da parede oposta. O arremesso e a recepção ocorrem a acima do solo.
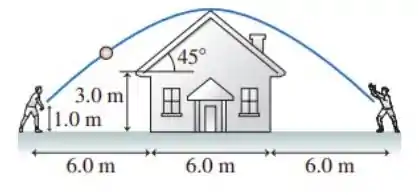
b) Em que ângulo você deve jogar a bola?
Ver solução completaQuestão 118
A areia se move sem escorregar a por uma esteira transportadora que está inclinada em . A areia entra em um tubo abaixo da extremidade da esteira, conforme mostrado na figura ao lado. Qual é a horizontal distância entre a correia transportadora e o tubo?
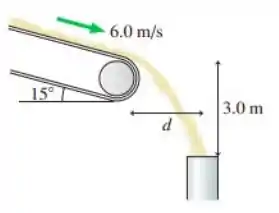
Questão 119
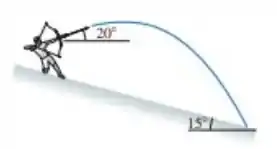
Um arqueiro parado em um declive de atira uma flecha acima do horizontal, conforme mostrado na figura ao lado. A que distância da encosta (alcance) a flecha atinge o solo se for atirada com uma velocidade de de um ponto que dista do solo?
Questão 120
Q - A trajetória de um projétil lançado do chão é dada pela equação
,
onde e são as coordenadas do projétil, medidas em metros. Se o vetor velocidade de lançamento do projétil é , em unidades do SI, o valor do parâmetro , em unidades de , é
Ver solução completaQuestão 121
Um canhão lança suas balas com uma certa inclinação em relação à horizontal. Assuma que a bala atinge o chão na mesma elevação em que foi lançada.
Se o tempo de voo foi de segundos, qual a componente vertical de sua velocidade inicial?
a) 50
b)
c)
d)
e) nenhuma das anteriores
Ver solução completaQuestão 122
Uma pedra é lançada fazendo um certo ângulo acima da horizontal. Considere o eixo-x, horizontal, positivo para a direita e o eixo-y, vertical, positivo para cima. Desprezando a resistência do ar, indique qual das sentenças abaixo é a verdadeira.
(A) A componente horizontal da velocidade permanece constante e a componente vertical da aceleração é igual a +g .
(B) A componente horizontal da velocidade permanece constante e a componente vertical da aceleração é igual a -g.
(C) A componente horizontal da velocidade permanece constante e a componente vertical da sua aceleração é igual a zero .
(D) As componentes verticais tanto da velocidade como da aceleração permanecem constantes.
(E) A componente vertical da velocidade permanece constante e não nula e a componente vertical da aceleração é igual a -g .
Ver solução completaQuestão 123
Três bolas são lançadas de um prédio alto com a mesma rapidez, mas em direções diferentes. A bola A é lançada na direção horizontal; a bola B, a 45° acima da horizontal e a bola C, a 45° abaixo da horizontal. Desprezando quaisquer efeitos devidos à resistência do ar, qual bola tem a maior rapidez um pouco antes de chocar-se com o solo?
A) A bola A
B) A bola B
C) A bola C
D) Todas as bolas têm a mesma rapidez.
E) As bolas B e C têm a mesma rapidez, que é maior que a rapidez da bola A.
Ver solução completaQuestão 125
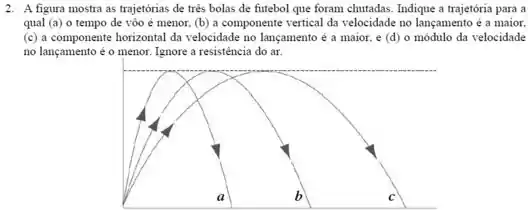
A figura mostra as trajetórias de três bolas de futebol que foram chutadas. Ignore a resistência do ar e considere as seguintes afirmações:
(I) o tempo de voo é o mesmo para todas as trajetórias;
(II) a trajetória corresponde à maior componente vertical da velocidade no lançamento;
(III) a componente vertical da velocidade no lançamento é a mesma para todas as trajetórias;
(IV) o módulo de velocidade de lançamento é o maior de todos para a trajetória ;
(V) o módulo de velocidade de lançamento é o maior de todos para a trajetória
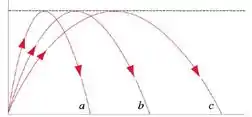
São verdadeiras as afirmações:
(A) I, III e IV
(B) II e V
(C) I, III e V
(D) II e IV
(E) III e V
Ver solução completaQuestão 126
Um canhão aponta numa direção que faz com a horizontal e dispara um projétil. Quando o projétil alcança o ponto mais alto de sua trajetória podemos afirmar que:
(A) Sua aceleração é zero.
(B) Sua velocidade é perpendicular à sua aceleração.
(C) Sua velocidade e sua aceleração são iguais a zero.
(D) A componente horizontal da sua velocidade é zero.
(E) A componente vertical e a componente horizontal de sua velocidade são iguais a zero.
Ver solução completaQuestão 127
Considere que um projétil é atirado do solo com uma velocidade de módulo , fazendo um ângulo com a direção horizontal, e atinja o topo de uma casa de altura acima do solo, após percorrer uma distância horizontal . Escolhe-se o eixo como horizontal e como vertical, orientado para cima. Das afirmações que se seguem, assinale aquela que é CORRETA.
- A aceleração média entre o instante de lançamento e aquele em que o projétil atinge o topo da casa é
- A distância horizontal percorrida é
- O projétil atinge o alto da casa com velocidade de módulo
- O tempo que o projétil leva para atingir a altura máxima é metade do tempo que leva para atingir o alto da casa
- A velocidade do projétil é nula no ponto de altura máxima
Questão 129
Uma bola é lançada do alto de um prédio com velocidade inicial de módulo fazendo um ângulo com a horizontal, onde e . Despreze
a resistência do ar e considere . Calcule o vetor velocidade da bola (em m/s) quando a sua distância horizontal ao ponto de partida é igual a .
Questão 130
Durante uma experiência em um laboratório de Física, um professor simula o lançamento de um projétil por um tanque de guerra, com velocidade e com um ângulo de lançamento em relação à horizontal. Sendo , e . Sabendo-se que durante o experimento o professor desprezou a resistência do ar, podemos afirmar que a altura máxima do projétil medida pela simulação foi
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 131
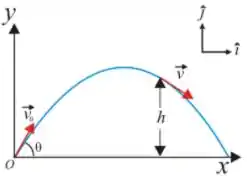
Q. Uma bola é lançada para o alto a partir da origem de um sistema cartesiano . A magnitude da velocidade inicial é e o ângulo de lançamento é . Quando a bola atinge a altura , como na figura, o vetor velocidade da bola é , com unidades no . Considerando a resistência do ar desprezível, a altura máxima alcançada pela bola, medida em metros, é:
Questão 132
Q - A trajetória de um projétil lançado do chão é dada pela equação
,
onde e são as coordenadas do projétil, medidas em metros. Se e , o módulo do vetor velocidade inicial do projétil, em metros por segundo, é:
Ver solução completaQuestão 133
Dois segundos após ter sido lançado, um projétil deslocou-se 40 na horizontal e 52 na
vertical, contados a partir do ponto de lançamento. As componentes horizontal e vertical da velocidade valem, respectivamente:
a) 20 m/s e 36 m/s
b) 20 m/s e 26 m/s
c) 40 m/s e 52 m/s
d) 20 m/s e 5,2 m/s
e) 40 m/s e 26 m/s
Ver solução completaQuestão 134
Considere o lançamento de projéteis num plano , onde o vetor aceleração pode ser escrito assim: . Sobre o movimento do projétil, marque a alternativa incorreta.
A. A velocidade do projétil ao longo da direção é constante;
B. A aceleração do projétil da direção é zero;
C. A velocidade do projétil ao longo da direção é constante;
D. A aceleração do projétil ao longo da direção é ;
E. A trajetória do projétil será uma parábola do tipo , onde , e são constantes.
Ver solução completaQuestão 135
Um corpo de massa é lançado no instante com velocidade de módulo do topo de uma mesa de altura com relação ao solo, conforme a figura abaixo. A altura máxima que o corpo atinge com relação ao solo é e o tempo que leva para o corpo atingir essa altura é . Além disso, o tempo total até o corpo atingir o solo é . Despreze efeitos oriundos da resistência do ar. Assumindo que , marque a resposta correta abaixo:
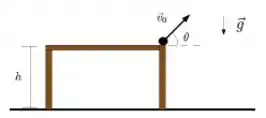
Dado: (capa da prova)
(a) ,,
(b) , ,
(c) , ,
(d) , ,
(e) , , .
Ver solução completaQuestão 136
Um sistema de coordenadas tem origem no solo de uma região plana horizontal, e dessa origem é lançado um projétil que faz um ângulo maior que zero com a horizontal. Ao passar por sua altura máxima o projétil tem uma velocidade e ao atingir o solo tem vetor posição . Podemos afirmar sobre os produtos escalares desses vetores com o vetor aceleração que
- e
- e
- e
- e
- e
Questão 137
Nas figuras abaixo, a parábola representa a trajetória de um lançamento oblíquo para , de um projétil nas proximidades da superfície da Terra. No ponto mais alto da trajetória do projétil, o diagrama que melhor representa os vetores velocidade e aceleração , neste ponto é: (despreze o efeito da resistência do ar)
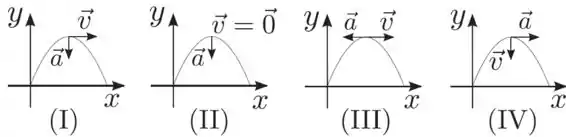
- (II)
- (I)
- (III)
- (IV)
- Nenhum dos diagramas
Questão 138
Um projétil é lançado, da superfície da Terra, com uma velocidade, de módulo conhecido e que faz um ângulo com a direção horizontal. Qual a afirmativa correta?
- O projétil atinge o solo com velocidade .
- No ponto de altura máxima, a velocidade do projétil é nula.
- Durante todo o trajeto até atingir o solo ele sofre a mesma aceleração.
- Durante todo o trajeto até atingir o solo ele possui velocidade de mesmo módulo.
- No ponto de altura máxima, a aceleração do projétil é nula.
Questão 139
Considere um projétil arremessado da origem no nível do solo ( e ) com velocidade inicial como descrito na figura.
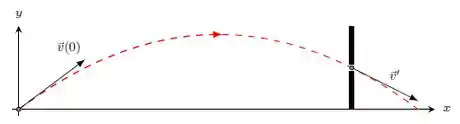
Dados:
a) Utilizando as equações horárias para e , mostre que
b) Encontre a distância percorrida no eixo até o instante onde a partícula retorna ao solo (não substitua a gravidade ).
Existe uma parede na posição , com um buraco localizado a uma altura com espaço suficiente para que o projétil o atravesse. Você pode utilizar o resultado dos itens anteriores. Considere que a gravidade é .
c) Encontre para que o projétil atravesse o buraco.
Ver solução completaQuestão 140
Um jogador de futebol chuta a bola de modo que o vetor velocidade inicial, , forma um ângulo com a direção horizontal. Despreze a resistência do ar e considere que a bola não sofre ação de outras forças além do campo gravitacional.
Considere , e
a) Suponha que e . Determine o módulo do vetor velocidade da bola, , para que a bola atinja a trave superior do gol.
b) Calcule o vetor velocidade em .
c) Calcule o instante de tempo em que a bola atinge a altura máxima.
d) Ao atingir a trave, a bola estava subindo ou descendo? Explique.
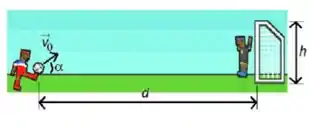
Questão 141
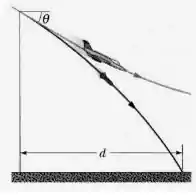
Um certo avião tem uma velocidade de 290,0 km/h e está mergulhando em um ângulo abaixo da horizontal quando o piloto libera um míssil despistador (figura abaixo). A distância horizontal entre o ponto de lançamento e o ponto onde a isca bate no solo é.
(a) Quanto tempo a isca fica no ar?
(b) De que altura ela foi liberada?
Questão 142
Durante erupções vulcânicas, grandes pedaços de rocha podem ser ejetados para fora do vulcão; estes
projeteis são chamados de bombas vulcânicas. A figura abaixo mostra a seção transversal do Monte Fuji, no Japão.
(a) Com que velocidade inicial uma bomba teria que ser ejetada, em um ângulo em relação à horizontal, a partir da abertura A, de modo a cair na base do vulcão em B, a uma distância vertical h = 3; 30 km e a uma distância horizontal d = 9; 40 km?
(b) Ignorando os efeitos do ar sobre o movimento da bomba, qual seria o tempo de voo?
(c) O efeito do ar aumentaria ou diminuiria sua resposta ao item (a)?