Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 10.Exercícios e Problemas - Ex. 36
|| Um cubo de gelo bem liso desliza dentro de um tubo horizontal liso com de diâmetro interno, descrevendo uma trajetória em um plano vertical. Na parte mais inferior do tubo, a velocidade do cubo de gelo é de .
Quanto vale a velocidade do cubo no topo?
Obtenha uma expressão algébrica para o módulo da velocidade do cubo quando este estiver em uma posição angular , onde este é um ângulo medido em sentido anti-horário a partir da parte inferior do tubo. Sua expressão deve resultar em e , e sua resposta ao item a, em .
Desenhe um gráfico de versus que cubra uma revolução inteira.
Passo 1
Essa questão exige uma atenção a mais em especial em trigonometria. Um esquema é:
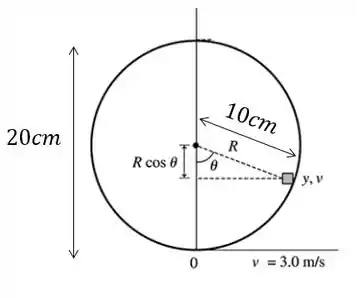
Passo 2
Quanto vale a velocidade do cubo no topo?
Podemos usar o princípio da conservação de energia mecânica e mudar os dados conforme necessidade:
Mas, em mecânica:
Assim:
Então:
Mas podemos por o em evidencia em ambos os lados e simplifica-lo.
Lembrando de passar de pra , e que num plano vertical o deslocamento vai ser exatamente o (é o nosso !)
Então, substituindo os termos ficamos com:
Passo 3
Obtenha uma expressão algébrica para o módulo da velocidade do cubo quando este estiver em uma posição angular, onde este é um ângulo medido em sentido anti-horário a partir da parte inferior do tubo. Sua expressão deve resultar em e , e sua resposta ao item a, em .
Nós podemos pegar a nossa expressão deduzida:
Tratar cada termos separado, assim:
Veja,
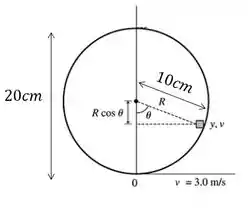
Por trigonometria o
Então nossa expressão fica:
Passo 4
Desenhe um gráfico de versus que cubra uma revolução inteira.
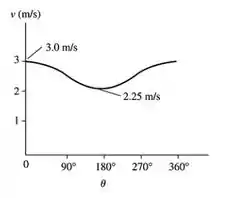
Pela expressão anterior o gráfico vai ser um cossenoide, dentro dos limites de velocidade:
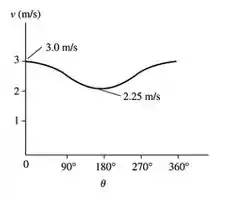
Resposta
