Enunciado
Física - Alaor Chaves- Ed: 1º - Capítulo 20.Exercícios e Problemas - Ex. 2
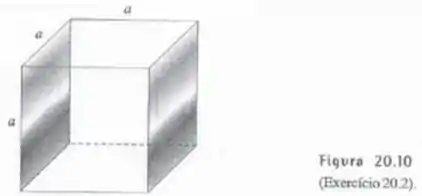
O cubo visto na Figura 20.10 tem duas faces metalizadas. O material do cubo tem resistividade muito maior que a do metal. Calcule a resistência elétrica entre as faces metalizadas.
Passo 1
Como a resistividade é constante, podemos escrever a resistência como
Nesse caso, o comprimento do “fio” é a aresta do cubo e a área da seção transversal é simplesmente . Assim,
Ou ainda,
PS: como a resistência do cubo é muito maior que a do metal, pudemos simplesmente esquecer a presença do metal para calcular essa resistência!
Resposta
Exercícios de Livros Relacionados
Um fio de cobre calibre 10 pode conduzir correntes até 30,0A . (a) Qual é a resistência de um fio de 100m de comprimento do fio? (b) Qual é o campo elétrico no fio quando a corrente é 30,0A ? (c) Quan
A que temperatura a resistência de um fio de cobre será 10% maior que sua resistência a 20 ° C ?
Seu aquecedor elétrico tem um elemento aquecedor de Nichrome com resistência de 8,00Ω a 20,0 ° C . Quando são aplicados 120V , a corrente elétrica aquece o fio de Nichrome a 1000 ° C . (a) Qual é a co
Você tem uma torradeira que usa fio de Nichrome como elemento aquecedor. Você precisa determinar a temperatura do fio em operação. Primeiramente você mede a resistência do elemento aquecedor a 20°C e
Determine uma expressão para a resistência entre as extremidades do semi-anel mostrado na Figura 25-51. A resistividade do material que constitui o anel é ρ .