Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 2.Problemas - Ex. 57

Daniel dirige na Estrada I-80 em Seward, no Estado de Nebraska, e segue por um trecho retilíneo de leste para oeste com uma velocidade média com módulo igual a 88   k m / h . Depois de percorrer 76   k m , ele atinge a saída de Aurora (Figura 2.44). Percebendo que foi longe demais, ele retorna   34   k m de oeste para leste até a saída para York com uma velocidade média com módulo igual a 72   k m / h . Para a viagem total desde Seward até a saída de York, qual é a) Sua velocidade escalar média? b) O módulo do vetor velocidade média?

Passo 1

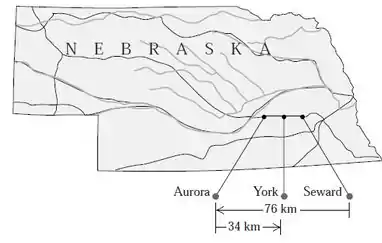
Opa! O enunciado nos dá o seguinte gráfico do estado de Nebraska nos estados unidos:

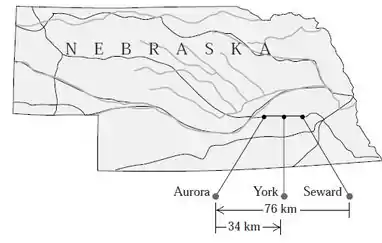
Bom, vamos analisar o que a questão nos pede:

O trajeto começa em Seward e tomamos que vai para uma direção positiva para Oeste.

Ele percorre 76 k m , percebe que andou muito e retonar 34 k m , nesse instante x = - 34 k m .

Sabemos que:

v e l o c i d a d e   m é d i a = d i s t â n c i a   p e r c o r r i d a t e m p o

Passo 2

  1. A distância percorrida é dado por:

    2. ∆ x = x f i n a l - x i n i c i a l

    ∆ x = 76 k m - ( - 34 k m )

    ∆ x = 110 k m

    Passo 3

    Para encontrar o tempo total percorrido, nós vamos usar:

    v m é d i a = ∆ x ∆ t

    Isso implica que de Seward a Auora ele leva o tempo de:

    t = ∆ x v m é d i a

    t S e w a r d → A u o r a = 76 k m 88 k m / h

    t S e w a r d → A u o r a = 0,8636 h

    Passo 4

    E de Auora para York:

    t A u o r a → Y o r k = - 34 k m - 72 k m / h

    t A u o r a → Y o r k = 0,4722 h

    O que implica em um tempo total de:

    t t o t a l = t S e w a r d → A u o r a + t A u o r a → Y o r k

    t t o t a l = 0,8636 h + 0,4722 h

    t t o t a l = 1,336 h

    Passo 5

    Assim, a velocidade média pode ser calculada:

    v m é d i a = 110 k m 1,336 h

    v m é d i a = 82 k m / h

    Passo 6

  2. Sabemos que:

v m é d i a = ∆ x ∆ t

E que ∆ x representa o deslocamento e não a distancia total percorrida.

Para toda viagem, ele acaba em:

∆ x = 76 k m - 34 k m = 42 k m

A oeste do seu ponto de partida.

Então, sua velocidade média nesse ponto é calcular por:

| v m é d i a | = 42 k m 1,336 h

| v m é d i a | = 31 k m / h

O movimento não é uniformemente na mesma direção, então o deslocamento é menor que a distância que viajou e a magnitude da velocidade média é menor que a velocidade média.

Resposta

  1. v m é d i a = 82 k m / h
  2. | v m é d i a | = 31 k m / h
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um trem com aceleração máxima a e desaceleração máxima f (magnitude da aceleração de freamento) tem de percorrer uma distância d entre duas estações. O maquinista pode escolher entre (a) seguir com a
Um jogador de shuffleboard usa um taco para imprimir a um disco uma aceleração constante, a partir do repouso, que faz o disco atingir uma velocidade de 6,0m / s após percorrer uma distância de 1,8m .
Um certo velocista é capaz de atingir uma velocidade máxima de 11,0m / s . Se o atleta parte do repouso com aceleração constante, atinge a velocidade máxima após percorrer uma distância de 12,0m . Em
Uma bolinha de gude é solta da borda de uma tigela em formato de meia-lua, com diâmetro de 50,0 cm, rola para baixo e depois para cima, até a borda oposta, em 10,0 s. Determine a) Avelocidade escalar
No ar ou no vácuo, a luz viaja a uma velocidade constante d e3,0x10 8m / s . Para responder a algumas das seguintes perguntas, se necessário, consulte os dados astronômicos no ApêndiceF. a) Um ano-luz