Enunciado
Física - Curso de Física Básica - Mecânica Volume 1 - 5ª Edição - Herch Moysés Nussenzveig- Ed: 5º - Capítulo 2.Problemas - Ex. 10
Um trem com aceleração máxima a e desaceleração máxima f (magnitude da aceleração de freamento) tem de percorrer uma distância d entre duas estações. O maquinista pode escolher entre (a) seguir com a aceleração máxima até certo ponto e a partir daí frear com a desaceleração máxima, até chegar; (b) acelerar até uma certa velocidade, mantê-la constante durante algum tempo e depois frear até a chegada. Mostre que a primeira opção é a que minimiza o tempo do percurso (sugestão: utilize gráficos v x t) e calcule o tempo mínimo de percurso em função de a, f e d.
Passo 1
Para mostrarmos que o caminho que minimiza é a opção vamos plotar os gráficos do trem.
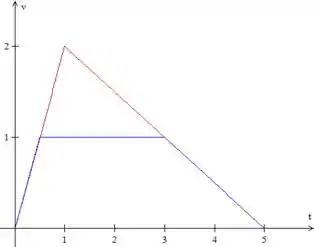
Nesse exemplo, vemos a situação a) em vermelho e a b) em azul, caso gastássemos o mesmo tempo utilizando os 2 métodos, a distância percorrida pelo método a) seria maior (área sob a curva maior). Se a gente notar, a aceleração e a desaceleração tem mesma magnitude entre os 2 gráficos, já que as declividades são iguais.
Caso a distância representasse a área sob o gráfico vermelho, o trapézio teria que se estender bem mais pro lado para alcançar essa área! E isso representaria um tempo maior.
Passo 2
Já que descobrimos que o método é mais eficiente vamos calcular o tempo necessário para percorrer .
Se olharmos para o gráfico vermelho podemos dividir a área em 2 triângulos retângulos menores(um à direita do vértice e outro à esquerda).
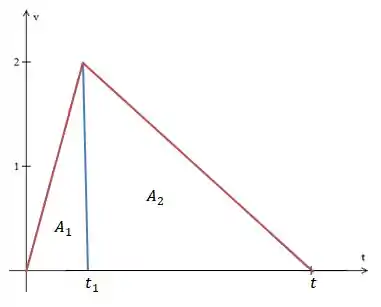
Supondo que sua área seja uma distância genérica , podemos dizer que será a soma dessas áreas:
A área do primeiro triângulo fica onde b é o tempo que o trem leva pra chegar na velocidade máxima (vértice do triângulo) e a altura é a velocidade máxima:
Já o segundo triângulo tem mesma altura que o primeiro ( e base , onde é o tempo total de deslocamento. Daí
Como
Como temos um fator indesejado que não sabemos, vamos utilizar a equação de desaceleração
Substituindo na nossa primeira equação obteremos