Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 2.Problemas - Ex. 55

A posição de uma partícula entre t = 0 e t = 2,0 s é dada por x ( t ) = ( 3,0   m / s 3 ) t 3 - ( 10,0   m / s 2 ) t 2 + ( 9,0   m / s ) t .

a) Faça gráficos de x t , v x t e a x t para essa partícula. b) Para que tempo(s) entre t = 0 e   t = 2,0 s a partícula está em repouso? O resultado obtido por você está de acordo com o gráfico v t da parte (a)? c) Para qual tempo calculado na parte (b) a aceleração da partícula é positiva ou negativa? Mostre que em cada caso podemos obter a mesma resposta pelo gráfico v x t ou pela função a x ( t ) . d) Para que tempo(s) entre t = 0 e   t = 2,0 s a velocidade da partícula não varia instantaneamente? Localize esse ponto nos gráficos a x t e v x t da parte (a). e) Qual a maior distância entre a partícula e a origem ( x = 0 ) no intervalo entre   t = 0 e   t = 2,0 s ? f) Para que tempo(s) entre t = 0 e   t = 2,0 s a partícula está aumentando de velocidade com a maior taxa? Para que tempo(s) entre   t = 0 e   t = 2,0 s a partícula está diminuindo de velocidade com a maior taxa? Localize esses pontos nos gráficos a x t e v x t da parte (a).

Passo 1

Opa, aqui temos uma formulinha que nos dá a posição de uma partícula em função do tempo: x t = 3,0 m s 3 t 3 - 10,0 m s 2 t 2 + 9,0 m s t

Essa fórmula vale pra t = 0 a t = 2,0 s . A primeira coisa que devemos fazer é os gráficos de x t , v x t e a x t para essa partícula.

Aqui, vamos encontrar a velocidade e a aceleração por meio de suas derivadas, que se dá respectivamente por:

v x t = d x d t

a x = d v x d t

Então, vamos relembrar como calcular derivada de potencia, seguindo a “regrinha do tombo”:

d ( t n ) d t = n ⋅ t n - 1 ,   p a r a   n ≥ 1

Passo 2

  1. O gráfico x ( t ) = ( 3,0   m / s 3 ) t 3 - ( 10,0   m / s 2 ) t 2 + ( 9,0   m / s ) t

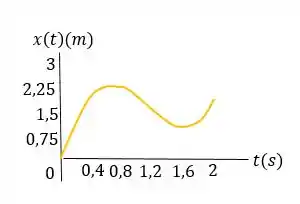
    2. Derivando a função em função de t : d x t d t temos que:

    v x t = d [ ( 3,0   m / s 3 ) t 3 - ( 10,0   m / s 2 ) t 2 + ( 9,0   m / s ) t ] d t

    v x t = 3 ⋅ ( 3,0 m / s 3 ) t 2 - 2 ⋅ ( 10 m / s 2 ) t + 9 m / s

    v x t = ( 9 m / s 3 ) t 2 - ( 20 m / s 2 ) t + 9 m / s

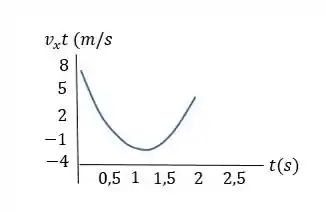
    Para encontrarmos a aceleração, derivamos novamente, ou seja, derivamos v x t = ( 9 m / s 3 ) t 2 - ( 20 m / s 2 ) t + 9 m / s

    a x t = d v x t d t = 2 ⋅ ( 9 m / s 3 ) t - 20 m / s 2

    a x t = ( 18 m / s 3 ) t - 20 m / s 2

    Passo 3

  2. Vamos analisar a partícula: ela esta instantaneamente em repouso quando sua velocidade for igual a zero, v x t = 0 .

    3. Então temos que v x t = ( 9 m / s 3 ) t 2 - ( 20 m / s 2 ) t + 9 m / s = 0

    Podemos encontrar o tempo resolvendo bhaskara:

    t = - b ± b 2 - 4 ⋅ a ⋅ c 2 ⋅ a

    Temos que: a = 9,0 ;   b = 20 ;   c = 9,0 . Então:

    t = ( 20 ± 20 2 - 4 9,0 ⋅ 9,0 s 18

    t = t 1 = 0,63 s t 2 = 1,59 s

    Observando os gráficos, podemos perceber que esse resultado, concorda com o gráfico v x t

    Passo 4

  3. Para t = 0,63 s , a aceleração fica:

    4. a x t = ( 18 m / s 3 ) t - 20 m / s 2

    a x = 18 m / s 3 ⋅ 0,63 s - 20 m / s 2

    a x = - 8,7 m / s 2

    Para t = 1,59 s :

    a x = 18 m / s 3 ⋅ 1,59 s - 20 m / s 2

    a x = + 8,6 m / s 2

    Em t = 0,63 s a inclinação do gráfico v x ( t ) é negativa, e em t = 1,59 s é positiva, entçao a mesma resposta é deduzida do gráfico v x ( t ) a partir da função a x ( t ) .

    Passo 5

  4. v x ( t ) não varia quando a aceleração é zero, a x = 0 .

    5. Isso ocorre em:

    t = 20 m / s 2 18 m / s 3

    t = 1,11 s

    Passo 6

  5. Quando a partícula esta mais distante da origem:

    6. v x = 0

    E a aceleração é menor que zero, a x < 0 . Nesse intante a partícula está começando a voltar para a origem.

    Esse é o caso para t = 0,63 s , que concorda com o gráfico x ( t ) , o que podemos observar que nesse instante, a posição da partícula é de x = 2,45 m .

    Passo 7

  6. A velocidade da partícula está mudando na maior parte das posições quando a aceleração é máxima.

O gráfico da aceleração nos mostra que isso acontece em t = 0 e em t = 2 s .

Como a velocidade é sempre positiva nesse intervalo de tempo, a partícula é acelerada na sua maior taxa quando a aceleração é positiva. E isso ocorre em t = 2 s

A partícula esta desacelerando em sua maior taxa quando a aceleração é negativa. E isso ocorre em t = 0 .

Resposta

  2. t = t 1 = 0,63 s t 2 = 1,59 s
  3. t = 0,63 s → a = n e g a t i v a ,

    4. e em t = 1,59 → a = p o s i t i v a .

  4. t = 1,11 s
  5. x = 2,45 m
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Você já deve ter percebido que a velocidade do seu carro não continua a aumentar, mesmo que você mantenha o pé pisando no acelerador. Isso se dá devido à resistência do ar e à fricção entre as partes
Um automóvel e um caminhão partem do repouso no mesmo instante, estando o automóvel uma certa distância atrás do caminhão. O caminhão possui aceleração constante de 2,10 m / s 2 e o automóvel de 3,40
Dois motoristas malucos dirigem de encontro um ao outro. No instante t = 0 , a distância entre os dois carros é D, o carro 1 está em repouso e o carro 2 se move da direita para a esquerda com velocida
Use as informações no Apêndice F para responder a estas perguntas. a) Qual é a velocidade das Ilhas Galápagos, localizadas na linha do Equador, em função do giro da Terra sobre o seupróprio eixo? b) Q
O maquinista de um trem de passageiros que viaja com velocidade v p = 25,0m / s avista um trem de carga cuja traseira se encontra a 200,0m de distância da frente do trem de passageiros (Figura 2.47).