Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight- Ed: 2º - Capítulo 2.Exercícios e Problemas - Ex. 66

66 . David está trafegando a constantes 30   m / s quando passa por Tina, que está sentada em seu carro estacionado. Ela começa a acelerar a uma taxa constante de 2,0   m / s 2 no exato instante da passagem de

David.

a . Que distância Tina percorrerá antes de passar por David?

  b . Qual será valor de sua velocidade ao passar por ele?

Passo 1

Um esquema é:

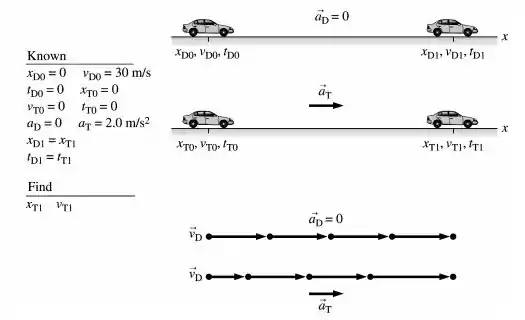
Lembre-se da tabelinha mil grau:

Passo 2

( a )

Para David e Tina:

x D 1 = x D 0 + v D 0 t D 1 - t D 0 + 1 2 a D t D 1 - t D 0 2 = v D 0 t D 1

x T 1 = x T 0 + v T 0 t T 1 - t T 0 + 1 2 a T t T 1 - t T 0 2 = 0 m + 0 m + 1 2 a T t T 1 2

Quando Tina passa por David, as distâncias são iguais e t D 1 =   t T 1 , então obtemos:

x D 1 = x T 1

⇒ v D 0 t D 1 = 1 2 a T t T 1 2

⇒ v D 0 = 1 2 a T t T 1

⇒ t D 1 = 2 v D 0 a T

⇒ t D 1 = 2 ( 30 m / s ) 2 m / s 2  

t D 1 = t T 1 = 30 s

Usando a equação de posição de Tina:

x T 1 = + 1 2 a T t T 1 2

= 1 2 ( 2 m / s 2 ) ⋅ 30 s 2

x T 1 = 900 m

Passo 3

( b ) A velocidade de Tina é:

v T 1 = v T 0 + a T t T 1 - t T 0

= ( 0 m / s ) + ( 2 m / s ) 2 ( 30 s - 0 s )

v T 1 = 60 m / s

Resposta

( a )

x T 1 = 900 m

( b )

v T 1 = 60 m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Você já deve ter percebido que a velocidade do seu carro não continua a aumentar, mesmo que você mantenha o pé pisando no acelerador. Isso se dá devido à resistência do ar e à fricção entre as partes
Um automóvel e um caminhão partem do repouso no mesmo instante, estando o automóvel uma certa distância atrás do caminhão. O caminhão possui aceleração constante de 2,10 m / s 2 e o automóvel de 3,40
Dois motoristas malucos dirigem de encontro um ao outro. No instante t = 0 , a distância entre os dois carros é D, o carro 1 está em repouso e o carro 2 se move da direita para a esquerda com velocida
Use as informações no Apêndice F para responder a estas perguntas. a) Qual é a velocidade das Ilhas Galápagos, localizadas na linha do Equador, em função do giro da Terra sobre o seupróprio eixo? b) Q
O maquinista de um trem de passageiros que viaja com velocidade v p = 25,0m / s avista um trem de carga cuja traseira se encontra a 200,0m de distância da frente do trem de passageiros (Figura 2.47).