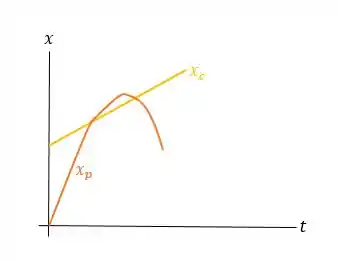
O maquinista de um trem de passageiros que viaja com velocidade v p = 25,0m / s avista um trem de carga cuja traseira se encontra a 200,0m de distância da frente do trem de passageiros (Figura 2.47). O trem de carga se desloca no mesmo sentido do trem de passageiros com velocidade v c = 15,0m / s . O maquinista imediatamente aciona o freio, produzindo uma aceleração constante igual a - 0,100m / s 2 , enquanto o trem de cargacontinua com a mesma velocidade. Considere x = 0 como o local onde se encontra a frente do trem de passageiros quando o freio é acionado. a) As vacas das vizinhanças assistirão a uma colisão? b) Caso a resposta anterior seja positiva, em que ponto ocorrerá a colisão? c) Faça um gráfico simples mostrando a posição da frente do trem de passageiros e a traseira do trem de carga.

22,5 s x p = 537 m da colisão e x c = 337 m da colisão.

Enunciado

Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 2.Problemas - Ex. 66

O maquinista de um trem de passageiros que viaja com velocidade s avista um trem de carga cuja traseira se encontra a de distância da frente do trem de passageiros (Figura 2.47). O trem de carga se desloca no mesmo sentido do trem de passageiros com velocidade . O maquinista imediatamente aciona o freio, produzindo uma aceleração constante igual a , enquanto o trem de carga

continua com a mesma velocidade. Considere como o local onde se encontra a frente do trem de passageiros quando o freio é acionado. a) As vacas das vizinhanças assistirão a uma colisão? b) Caso a resposta anterior seja positiva, em que ponto ocorrerá a colisão? c) Faça um gráfico simples mostrando a posição da frente do trem de passageiros e a traseira do trem de carga.

Passo 1

Oi, galerinha! Tudo bom? Para a gente saber se os trens colidiram, temos que verificar se existem um tempo , onde ambos os trens ocupam a mesma posição.

Para isso vamos aplicar a equação da posição ao movimento de cada trem:

Mas antes precisamos adotar algumas referências. Seja o trem de passageiro e o trem de carga.

Para a frente do trem de passageiro, , e .

Já para o trem de carga, (pois é a distância que ele está do trem e tomamos ele como marco zero), e (pois ele segue em velocidade constante).

Bora aplicar agora!

Passo 2

Vamos começar pelo trem . Vamos aplicar:

Já para o trem , vamos aplicar a equação do M.U:

Para termos o momento de colisão, temos que igualhar as duas posições:

Então,

Substituindo os dados do problema,

Para que possamos descobrir o valor de , vamos fazer um Bhaskara:

A colisão ocorre no menor tempo, ou seja, em:

Passo 3

Agora que já sabemos o instante da colisão, , vamos aplicar

Substituindo,

O trem de passageiros se move antes da colisão.

Para o trem de carga, podemos apenas calcular a diferença da distância inicial deles.

antes da colisão.

Passo 4

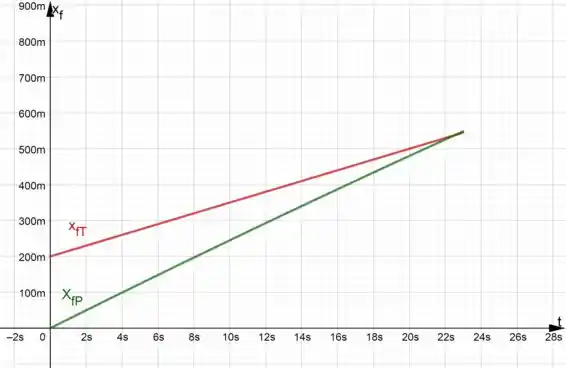
A segunda raiz da equação para é o tempo que os trens se encontrariam novamente se eles estavam em trilhas paralelas e continuou sua moção após o primeiro encontro:

Resposta

da colisão e da colisão.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

É possível disparar uma flecha a uma velocidade tão elevada como 100 m/s.Se o atrito pudesse ser ignorado, a que altura uma flecha lançada nessa velocidade subiria se fosse atirada em linha reta para

Um caminhão percorre 40,0m em 8,50s enquanto reduz sua velocidade lentamente até chegar ao final a 2,80m / s . Descubra sua velocidade original.Calcule sua aceleração.

A distância mínima necessária para parar um carro movendo-se a 35,0 mi/h é 40,0 pés. Qual é a distância mínima para parar o mesmo carro em movimento a 70,0 mi/h, supondo a mesma taxa de aceleração?Dad

Uma bola acelera a partir do repouso a 0,500 m/s2 enquanto se move para baixo em um plano inclinado de 9,00 m de comprimento. Quando atinge o fundo, a bola rola para outro plano, ao qual chega em repo

Mostre que as maiores e menores acelerações médias da Tabela 2.3 estão corretamente calculadas a partir dos intervalos de tempo medidos necessários para os carros acelerarem de 0a60m i / h .Converta a