Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 2.Problemas - Ex. 70

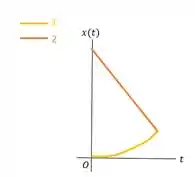
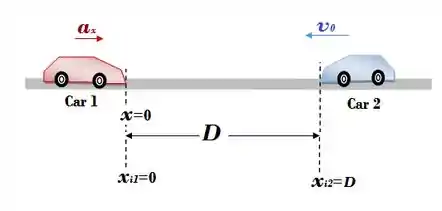
Dois motoristas malucos dirigem de encontro um ao outro. No instante t = 0 , a distância entre os dois carros é D, o carro 1 está em repouso e o carro 2 se move da direita para a esquerda com velocidade v 0 . O carro 1 começa a acelerar a partir de t = 0 com aceleração constante a x . O carro 2 continua a se mover com velocidade constante. a) Em que instante ocorrerá a colisão? b) Ache a velocidade do carro 1 imediatamente antes de colidir com o carro 2. c) Faça diagramas x t e v x t para o carro 1 e para o carro 2. Desenhe curvas para cada veículo usando o mesmo eixo.

Passo 1

Oi, galerinha! Tudo bom? Nessa questão não temos valores para substituir, então temos que estabelecer relações para as variáveis fornecidas pelo problema.

Aqui temos uma situação de colisão. Nessas situações é importante escolhermos um referencial e a partir dele construímos as equações do movimento para cada carro.

Vamos aplicar as equações de aceleração constantes ao movimento de cada carro. A colisão ocorre quando o os carros estão no mesmo lugar ao mesmo tempo.

Vamos tomar + x para a direita.

A localização do carro 1 é: x = 0 . Então x 01 = 0 e x 02 = D .

Os carros colidem quando:

x 1 = x 2

Passo 2

  1. Pela equação do MUV, temos

    2. x - x 0 = v 0 ⋅ t + a x ⋅ t 2 2

    x é a posição no tempo t , x 0 é a posição incial, v 0 é a velocidade inicial e a x é a aceleração.

    Precisamos calcular os deslocamentos!

    Para o carro 1, x 0 = 0 , logo

    x 1 = a x ⋅ t 2 2

    Para o carro 2, x 0 = D , logo

    x 2 = D - v 0 ⋅ t

    A velocidade é negativa pois é o sentido contrario ao adotado como sentido positivo da situação.

    E igualar essas duas equações:

    a x ⋅ t 2 2 = D - v 0 ⋅ t

    Vamos igualar a zero e encontrar o tempo, t , (por bhaskara):

    a x ⋅ t 2 2 + v 0 ⋅ t - D = 0

    ⇒     t = 1 a x - v 0 ± v 0 2 + 2 ⋅ a x ⋅ D

    Vamos considerar somente a raiz positiva, então:

    t = 1 a x - v 0 + v 0 2 + 2 ⋅ a x ⋅ D

    Passo 3

  2. Para encontrarmos a velocidade do carro 1 imediatamente antes da colisão é dada por:

    3. v 1 = a x ⋅ t

    Substituindo o tempo encontrado no Passo 1, ficamos com

    v 1 = a x 1 a x - v 0 + v 0 2 + 2 ⋅ a x ⋅ D

    Simplificando,

    v 1 = v 0 2 + 2 a x ⋅ t - v 0

    Passo 4

  3. Quando, a x = 0 , D - v 0 ⋅ t = 0 e t = D v 0 é o tempo que leva de carro 2 para percorrer a distância D.

Quando v 0 = 0 ,   t = 2 D a x , o tempo que o carro 1 viaja numa distancia D.

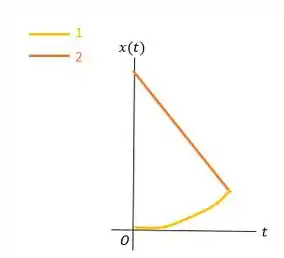
Resposta

  1. t = 1 a x - v 0 + v 0 2 + 2 ⋅ a x ⋅ D
  2. v 1 = a x ⋅ t = v 0 2 + 2 a x ⋅ t - v 0

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Aposição de uma partícula entre t = 0 e t = 2,0 s é dada por x ( t ) = ( 3,0m / s 3 ) t 3 - ( 10,0m / s 2 ) t 2 + ( 9,0m / s ) t . a) Faça gráficos de x t , v x t e a x t para essa partícula. b) Para
Quando aplicamos as equações cinemáticas para um corpo movimentando-se em uma dimensão, qual das afirmações a seguir deve ser verdadeira?a) A velocidade do corpo tem de permanecer constante.b) A acele
Um skatista começa do repouso e se move morro abaixo com aceleração constante em linha reta, movendo-se por 6 s. Em uma segunda tentativa, ele começa do repouso e se move ao longo da mesma linha reta
Um caminhão em uma estrada reta parte do repouso, acelerando a 2,00m / s 2 até atingir uma velocidade de 20,0 m/s. O caminhão viaja então por 20,0 s com velocidade constante, até que os freios são aci
No Exemplo 2.7, investigamos um jato pousando em um navio porta-aviões. Em uma manobra realizada depois, o jato chega para pouso em terra firme com velocidade de 100 m/s, e sua aceleração pode ter int