Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 2.Problemas - Ex. 69
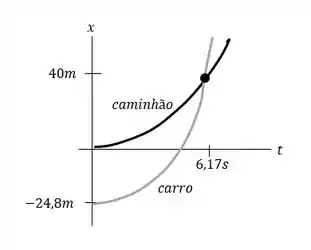
Um automóvel e um caminhão partem do repouso no mesmo instante, estando o automóvel uma certa distância atrás do caminhão. O caminhão possui aceleração constante de e o automóvel de . O automóvel ultrapassa o caminhão depois que o caminhão se deslocou . a) Qual o tempo necessário para que o automóvel ultrapasse o caminhão? b) Qual era a distância inicial do automóvel em relação ao caminhão? c) Qual a velocidade desses veículos quando eles estão lado a lado? d) Em um único diagrama, desenhe a posição de cada veículo em função do tempo. Considere como a posição inicial do caminhão.
Passo 1
Olá, meu amigo. Yuri aqui e estarei te ajudando a resolver essa atividade.
Vamos esboçar o que esta acontecendo na situação do exercício:
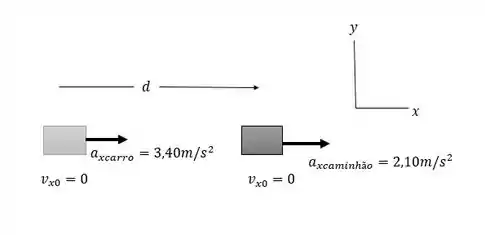
Basicamente temos uma situação de ultrapassagem.
Vamos tomar as coordenadas como na posição inicial do caminhão.
Seja a distância que o carro inicialmente está atrás do caminhão, então:
E
Seja o tempo leva o auto para pegar o caminhão. Assim, no tempo , o caminhão passou por um deslocamento:
Então,
O carro encontra o caminhão, assim, no momento , este também está em .
Passo 2
- Vamos usar o momento do caminhão para calcular :
- Vamos usar o momento do carro para calcular :
- A posições dos carros são dadas por:
Sabemos que:
é a posição, é a posição inicial, é a velocidade inicial, a aceleração inicial e o tempo.
Assim:
Passo 3
Assim, vamos igualar as equações:
Passo 4
Passo 5
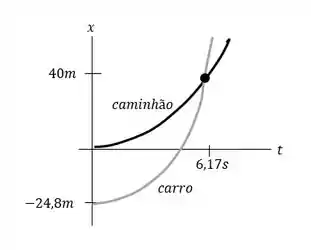
Na parte (c), descobrimos que o carro estava viajando mais rápido do que o caminhão quando eles chegavam. O gráfico concorda com isso: na interseção das duas curvas a inclinação para o carro é maior que a do caminhão. O automóvel deve ter uma velocidade média maior que a do caminhão, uma vez que viaja mais longe no mesmo intervalo de tempo.
Resposta
