Enunciado
Física - Moysés - Vol. 4 - Ed: 1º - Capítulo 2.Problemas - Ex. 16
Deduza a equação (2.42) para uma lente delgada construindo a imagem por duas refrações sucessivas, nas superfícies esféricas dianteira e traseira da lente.
Passo 1
Legal, nesse problema temos que deduzir a equação das lentes delgadas construindo a imagem por duas refrações sucessivas por superfícies refratoras esféricas (seção 2.7). Sabemos que quando a luz atravessa ums superfície refratora esférica de um meio com índide de refração para um meio com índice de refração , temos que
Nessa expressão, é a distância do objeto até a superfície, a distância da imagem até a superfície (dentro dela) e é o raio de curvatura do superfície esférica.
Nesse problema vamos aplicar essa fórmula duas vezes. Primeiro vamos analisar a refração pela superfície esférica dianteira da lente:
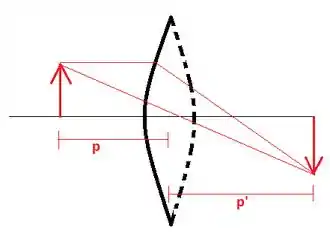
Note que eu representei a superfície traseira em pontilhado por enquanto. Também usei no lugar de . Usando a expressão, temos que
Aqui eu também usei que o raio da superfície dianteira é . Com isso, temos que
Passo 2
Agora vamos considerar a refração da imagem formada no passo 1 pela superfície traseira:
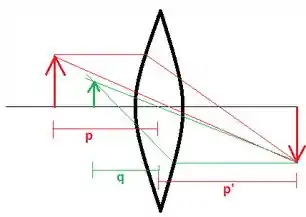
É importante ressaltar que os desenhos tem apenas caráter ilustrativo, não representando adequadamente a formação das imagens.
Considerando essa segunda refração, em que agora o objeto é virtual, temos que
Como agora passamos do meio com índice para o meio com índice , fica do lado direito da equação. Usamos na expressão pois o objeto dessa refração é virtual. Com isso, temos que
Passo 3
Igualando as equações dos passos 1 e 2:
Portanto,
Ou ainda,
Por fim,
Essa é exatamente a equação 2.42.
Resposta
Demonstração.