Enunciado
Física - Moysés - Vol. 4 - Ed: 1º - Capítulo 2.Problemas - Ex. 21
Uma lente delgada convergente de distância focal é colocada entre um objeto e um anteparo fixos, a uma distância um do outro. Desloca-se a lente até que ela forma uma imagem nítida do objeto no anteparo.
a) Mostre que existem duas posições diferentes da lente para as quais isso acontece.
b) Sejam e os tamanhos da imagem correspondentes a essas duas posições. Demonstre que o tamanho do objeto é a média geométrica de e .
Passo 1
O primeiro passo sempre é fazer um esquema do problema:
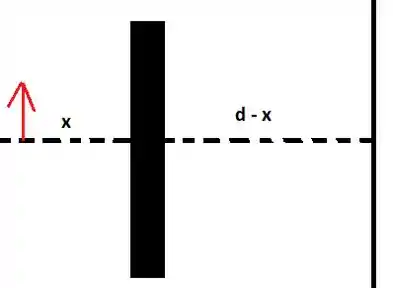
A distância do objeto até a lente é e a distância da lente até o anteparo é . A equação das lentes diz que
Nesse caso, e . Assim,
Portanto,
Ou ainda,
Passo 2
Resolvendo essa equação do segundo grau em , achamos que
Como , temos que
Vemos que existem duas posições em que podemos colocar a lente:
Passo 3
Para o item (b), temos que lembrar que o aumento lateral é
No caso, para , temos que o tamanho da imagem é . Já para , temos que o tamanho da imagem é . Daí,
Com isso,
Agora veja que
Portanto,
Logo,
Com isso,
Vemos que é a média geométrica de e .
Resposta
Demonstração.