Dentro do carro, um motorista atira verticalmente para cima um ovo, que atinge uma altura máxima justo abaixo do teto, 65 cm acima do ponto de lançamento. Ele recupera o ovo na mesma altura de lançamento. Se você está na beira da estrada e mede a distância horizontal entre os pontos de largada e de pegada, encontrando 19 m, (a) qual é a rapidez do carro? (b) Neste seu referencial, a que ângulo acima da horizontal o ovo foi lançado?

E aí pessoal, beleza? Bom, nesse problema acontece algo interessante. O motorista vê algo como um movimento retilíneo, já o observador de fora vê um lançamento oblíquo. Sabendo dessas informações podemos analisar bem a questão.

Vamos analisar o movimento que o observador vê:

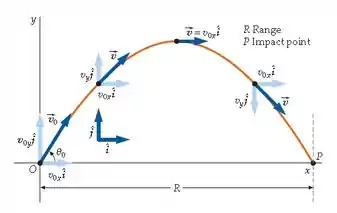
Nos é dito que a distância horizontal é de 19 m, então:

Sabemos também que e como , temos que que é exatamente a velocidade do carro.

Bom, então precisamos do tempo do movimento para encontrar essa velocidade que é o que queremos. E nos foi dito que a altura máxima é de 65 cm.

Vamos analisar somente o movimento de subida:

Se queremos o tempo do movimento total, temos que somar o tempo de subida com o de descida. Porém esses tempos são iguais então:

Então: